Euclidean domain

Commutative algebra | Ring theory

In mathematics, more specifically in ring theory, a Euclidean domain (also called a Euclidean ring) is an integral domain that can be endowed with a which allows a suitable generalization of the Euclidean division of integers. This generalized Euclidean algorithm can be put to many of the same uses as Euclid's original algorithm in the ring of integers: in any Euclidean domain, one can apply the Euclidean algorithm to compute the greatest common divisor of any two elements. In particular, the greatest common divisor of any two elements exists and can be written as a linear combination of them (Bézout's identity). Also every ideal in a Euclidean domain is principal, which implies a suitable generalization of the fundamental theorem of arithmetic: every Euclidean domain is a unique factorization domain. It is important to compare the class of Euclidean domains with the larger class of principal ideal domains (PIDs). An arbitrary PID has much the same "structural properties" of a Euclidean domain (or, indeed, even of the ring of integers), but when an explicit algorithm for Euclidean division is known, one may use the Euclidean algorithm and extended Euclidean algorithm to compute greatest common divisors and Bézout's identity. In particular, the existence of efficient algorithms for Euclidean division of integers and of polynomials in one variable over a field is of basic importance in computer algebra. So, given an integral domain R, it is often very useful to know that R has a Euclidean function: in particular, this implies that R is a PID. However, if there is no "obvious" Euclidean function, then determining whether R is a PID is generally a much easier problem than determining whether it is a Euclidean domain. Euclidean domains appear in the following chain of class inclusions: rngs ⊃ rings ⊃ commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ GCD domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ ⊃ fields ⊃ algebraically closed fields (Wikipedia).

RNT2.3. Euclidean Domains

Ring Theory: We define Euclidean domains as integral domains with a division algorithm. We show that euclidean domains are PIDs and UFDs, and that Euclidean domains allow for the Euclidean algorithm and Bezout's Identity.

From playlist Abstract Algebra

Abstract Algebra | Introduction to Euclidean Domains

We give the definition of a Euclidean domain, provide some examples including the Gaussian Integers Z[i], and prove that every Euclidean domain is a principal ideal domain (PID). Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.mi

From playlist Abstract Algebra

Lecture 9. GCDs

From playlist Abstract Algebra 2

Geometry: Introduction to the Polygon (quadrilateral, pentagon, hexagon and more)

Learn the definition of polygon - a very important shape in geometry. When a polygon has a small number of sides, there is a word you use instead of "polygon". We teach you the names of polygons with 3 to 10 sides. To learn more Geometry, you can watch our playlist from the beginning:

From playlist Euclidean Geometry

MAST30026 Lecture 2: Examples of spaces (Part 1)

I started with the definition of a metric space, we briefly discussed the example of Euclidean space (proofs next time) and then I started to explain a few natural metrics on the circle. Lecture notes: http://therisingsea.org/notes/mast30026/lecture2.pdf The class webpage: http://therisin

From playlist MAST30026 Metric and Hilbert spaces

Exploring Symplectic Embeddings and Symplectic Capacities

Speakers o Alex Gajewski o Eli Goldin o Jakwanul Safin o Junhui Zhang Project Leader: Kyler Siegel Abstract: Given a domain (e.g. a ball) in Euclidean space, we can ask what is its volume. We can also ask when one domain can be embedded into another one without distorting volumes. These

From playlist 2019 Summer REU Presentations

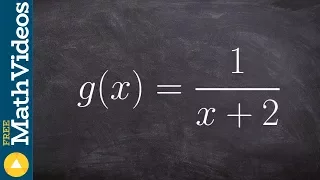
Domain of a simple rational function in interval and set notation

👉 Learn how to find the domain of rational functions. Recall that the domain of a function is the set of possible input values (x-values) of the function. For a rational function, the denominator cannot be zero. Thus, to find the domain of a rational function, we first find the values of x

From playlist Domain of a function with a fraction | Linear

Determine the Domain of Various Functions

This video explains how to determine the domain of various functions including linear, quadratic, square root, cube root, cubic, absolute value, and rational functions. http://mathispower4u.com

From playlist The Properties of Functions

The Domain of Rational and Square Root Functions

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Domain of Rational and Square Root Functions

From playlist College Algebra

Commutative algebra 9 (Euclidean domains)

This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We describe one method of visualizing rings by drawing pictures of their points, and use this to show that the ring of Gaussia

From playlist Commutative algebra

Visual Group Theory: Lecture 7.5: Euclidean domains and algebraic integers

Visual Group Theory: Lecture 7.5: Euclidean domains and algebraic integers. Around 300 BC, the Greek mathematician Euclid found an algorithm to compute the greatest common divisor (gcd) of two numbers. Loosely speaking, a Euclidean domain is a commutative ring for which this algorihm stil

From playlist Visual Group Theory

Rings and modules 4 Unique factorization

This lecture is part of an online course on rings and modules. We discuss unique factorization in rings, showing the implications (Integers) implies (Euclidean domain) implies (Principal ideal domain) implies (Unique factorization domain). We give a few examples to illustrate these implic

From playlist Rings and modules

Lecture 8. PIDs and Euclidean domains

From playlist Abstract Algebra 2

Abstract Algebra | Summary of Integral Domains

We give a summary of different types of integral domains with examples and non-examples. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net Randolph College Math: http://www.randolphcollege.edu/mathematics/ Research

From playlist Abstract Algebra

Guofang Wei - Fundamental Gap Estimate for Convex Domains - IPAM at UCLA

Recorded 07 February 2022. Guofang Wei of the University of California, Santa Barbara Mathematics presents "Fundamental Gap Estimate for Convex Domains" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: In their celebrated work, B. Andrews and J. Clutterbuck

From playlist Workshop: Calculus of Variations in Probability and Geometry

Existence Of Maximal Ideals - Feb 05, 2021- Rings and Modules

In this video we show using the axiom of choice that rings have maximal ideals.

From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Worldwide Calculus: Euclidean Space

Lecture on 'Euclidean Space' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.

From playlist Multivariable Spaces and Functions

Euclidean domain

Related pages