
Rings and modules 5 Examples of unique factorizations
This lecture is part of an online course on rings and modules. We give some examles to illustrate unique factorization. We use the fact that the Gaussian integers have unique factorization to prove Fermat's theorem about primes that are sums o 2 squares. Then we discuss a few other quadra
From playlist Rings and modules

Abstract Algebra | Introduction to Unique Factorization Domains
We introduce the notion of a unique factorization domain (UFD), give some examples and non-examples, and prove some basic results. Integral Domain Playlist: https://www.youtube.com/playlist?list=PL22w63XsKjqxPO6pQ8wiZcIrtpTznGSre Please Subscribe: https://www.youtube.com/michaelpennmath?
From playlist Abstract Algebra

Rings and modules 4 Unique factorization
This lecture is part of an online course on rings and modules. We discuss unique factorization in rings, showing the implications (Integers) implies (Euclidean domain) implies (Principal ideal domain) implies (Unique factorization domain). We give a few examples to illustrate these implic
From playlist Rings and modules

Unique factorization and its difficulties I Data Structures in Mathematics Math Foundations 198
The Unique Factorization Theorem is also called the Fundamental Theorem of Arithmetic: the existence and uniqueness of a prime factorization for a natural number n. It is a pillar of number theory, and goes back to Euclid. We want to have a look at the logical structure of this theorem.
From playlist Math Foundations

Unique factorization and its difficulties II | Data Structures Math Foundations 199
We continue with our discussion of the Fundamental Theorem of Arithmetic, which is that any natural number is uniquely factorizable in to primes. But this is not exactly true, at least not if we allow such big numbers as z into our realm of natural numbers! In this video we look at the ac
From playlist Math Foundations
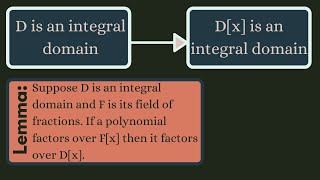
Abstract Algebra | If D is a UFD then D[x] is a UFD.
We prove an important result that states the ring of polynomials whose coefficients are from a unique factorization domain is itself a unique factorization domain. Along the way, we define the content of a polynomial, prove Gauss' lemma, and prove that if a polynomial factors over the fiel
From playlist Abstract Algebra

This lecture is part of an online course on rings and modules. We review basic properties of polynomials over a field, and show that polynomials in any number of variables over a field or the integers have unique factorization. For the other lectures in the course see https://www.youtu
From playlist Rings and modules
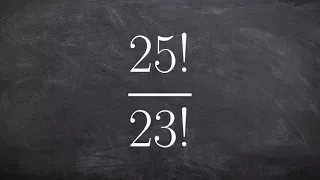
Simplifying a factorial divided by another factorial
👉 Learn all about factorials. Factorials are the multiplication of a number in descending integer values back to one. Factorials are used often in sequences, series, permutations, and combinations. Factorial quotient expressions are simplified by canceling out common integer products or
From playlist Sequences

👉 Learn all about factorials. Factorials are the multiplication of a number in descending integer values back to one. Factorials are used often in sequences, series, permutations, and combinations. Factorial quotient expressions are simplified by canceling out common integer products or
From playlist Sequences

Dedekind domains: Introduction
This lecture is part of an online graduate course on commutative algebra, and is an introduction to Dedekind domains. We define Dedekind domains, and give several examples of rings that are or are not Dedekind domains. This is a replacement video: as several alert viewers pointed out, t
From playlist Commutative algebra

Commutative algebra 9 (Euclidean domains)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We describe one method of visualizing rings by drawing pictures of their points, and use this to show that the ring of Gaussia
From playlist Commutative algebra

Commutative algebra 10 (Weierstrass preparation theorem)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we describe a second method of visualizing rings by drawing a point for each basis element of the ring. We giv
From playlist Commutative algebra

Lecture 8. PIDs and Euclidean domains
From playlist Abstract Algebra 2

Visual Group Theory: Lecture 7.4: Divisibility and factorization
Visual Group Theory: Lecture 7.4: Divisibility and factorization The ring of integers have a number of properties that we take for granted: every number can be factored uniquely into primes, and all pairs of numbers have a unique gcd and lcm. In this lecture, we investigate when this happ
From playlist Visual Group Theory

