
Group theory 7: Semidirect products
This is lecture 7 of an online course on group theory. It covers semidirect products and uses them to classify groups of order 6.
From playlist Group theory

Inner & Outer Semidirect Products Derivation - Group Theory
Semidirect products are a very important tool for studying groups because they allow us to break a group into smaller components using normal subgroups and complements! Here we describe a derivation for the idea of semidirect products and an explanation of how the map into the automorphism
From playlist Group Theory

Groups in abstract algebra examples
In this tutorial I discuss two more examples of groups. The first contains four elements and they are the four fourth roots of 1. The second contains only three elements and they are the three cube roots of 1. Under the binary operation of multiplication, these sets are in fact groups.
From playlist Abstract algebra

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys The Klein Four-Group is the smallest noncyclic abelian group. Every proper subgroup is cyclic. We look at the the multiplication in the Klein Four-Group and find all of it's subgroups.
From playlist Abstract Algebra

Definition of a group Lesson 24
In this video we take our first look at the definition of a group. It is basically a set of elements and the operation defined on them. If this set of elements and the operation defined on them obey the properties of closure and associativity, and if one of the elements is the identity el
From playlist Abstract algebra

Walter van Suijlekom: Semigroup of inner perturbations in Non Commutative Geometry
Starting with an algebra, we define a semigroup which extends the group of invertible elements in that algebra. As we will explain, this semigroup describes inner perturbations of noncommutative manifolds, and has applications to gauge theories in physics. We will present some elementary e
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

AlgTopReview4: Free abelian groups and non-commutative groups
Free abelian groups play an important role in algebraic topology. These are groups modelled on the additive group of integers Z, and their theory is analogous to the theory of vector spaces. We state the Fundamental Theorem of Finitely Generated Commutative Groups, which says that any such
From playlist Algebraic Topology
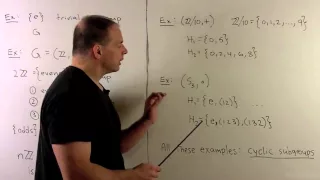
Abstract Algebra: We define the notion of a subgroup and provide various examples. We also consider cyclic subgroups and subgroups generated by subsets in a given group G. Example include A4 and D8. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-
From playlist Abstract Algebra

"New Paradigms in Invariant Theory" - Roger Howe, Yale University [2011]
HKUST Institute for Advanced Study Distinguished Lecture New Paradigms in Invariant Theory Speaker: Prof Roger Howe, Yale University Date: 13/6/2011 Video taken from: http://video.ust.hk/Watch.aspx?Video=6A41D5F6B1A790DC
From playlist Mathematics

Abstract Algebra: We introduce the notion of a group and describe basic properties. Examples given include familiar abelian groups and the symmetric groups. U.Reddit course materials available at http://ureddit.com/class/23794/intro-to-group-theory Master list at http://mathdoctorbob.o
From playlist Abstract Algebra

BAG1.4. Toric Varieties 4 - Spec(R) and Affine Semigroups
Basic Algebraic Geometry: In this part, we introduce Spec(R) and affine semigroups. This allows us to give yet another characterization of affine toric varieties in terms of affine semigroups.
From playlist Basic Algebraic Geometry

The potential of AI, illustrated in the classification of finite..(Lecture 5) by Carlos Simpson
INFOSYS-ICTS RAMANUJAN LECTURES EXPLORING MODULI SPEAKER: Carlos Simpson (Université Nice-Sophia Antipolis, France) DATE: 10 February 2020 to 14 February 2020 VENUE: Madhava Lecture Hall, ICTS Campus Lecture 1: Exploring Moduli: basic constructions and examples 4 PM, 10 February 2020
From playlist Infosys-ICTS Ramanujan Lectures
Type Classes for Mathematical Formalizations in Coq - Matthieu Sozeau
Matthieu Sozeau INRIA Paris; Member, School of Mathematics October 3, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Zero dimensional valuations on equicharacteristic (...) - B. Teissier - Workshop 2 - CEB T1 2018
Bernard Teissier (IMJ-PRG) / 06.03.2018 Zero dimensional valuations on equicharacteristic noetherian local domains. A study of those valuations based, in the case where the domain is complete, on the relations between the elements of a minimal system of generators of the value semigroup o
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Markus Haase : Operators in ergodic theory - Lecture 3 : Compact semigroups and splitting theorems
Abstract : The titles of the of the individual lectures are: 1. Operators dynamics versus base space dynamics 2. Dilations and joinings 3. Compact semigroups and splitting theorems Recording during the thematic meeting : "Probabilistic Aspects of Multiple Ergodic Averages " the December 8
From playlist Dynamical Systems and Ordinary Differential Equations

Workshop 1 "Operator Algebras and Quantum Information Theory" - CEB T3 2017 - A.Gheondea
Aurelian Gheondea (Bilkent University, Ankara) / 11.09.17 Title: Symmetry versus Conservation Laws in Dynamical Quantum Systems: A Unifying Approach through Propagation of Fixed Points Abstract: We unify recent Noether type theorems on the equivalence of symmetries with conservation laws
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

On the structure of quantum Markov semigroups - F. Fagnola - PRACQSYS 2018 - CEB T2 2018
Franco Fagnola (Department of Mathematics, Politecnico di Milano, Italy) / 06.07.2018 On the structure of quantum Markov semigroups We discuss the relationships between the decoherence-free subalgebra and the structure of the fixed point subalgebra of a quantum Markov semigroup on B(h) w
From playlist 2018 - T2 - Measurement and Control of Quantum Systems: Theory and Experiments

From Magmas to Fields: a trippy excursion through algebra - SoME2 3b1b
A gentle introduction to the most basic definitions in Algebra (and how to make them stick forever). If you always struggled to remember what a field is this video is for you. You will learn about: 0:00 This videos aim 1:20 Sets 1:52 Magmas 3:15 Semigroups 4:39 Monoids 5:22 Groups 6:04 Co
From playlist Summer of Math Exposition 2 videos

Counting and dynamics in SL2 - Michael Magee
Michael Magee Member, School of Mathematics April 6, 2015 In this talk I'll discuss a lattice point count for a thin semigroup inside SL2(ℤ)SL2(Z). It is important for applications I'll describe that one can perform this count uniformly throughout congruence classes. The approach to count
From playlist Mathematics
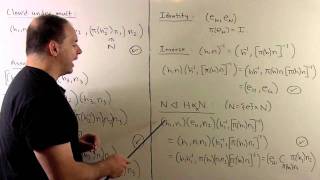
EDIT: At 6:24, the product should be "(e sub H, e sub N)", not "(e sub H, e sub G)" Abstract Algebra: Using automorphisms, we define the semidirect product of two groups. We prove the group property and construct various examples, including the dihedral groups. As an application, we
From playlist Abstract Algebra