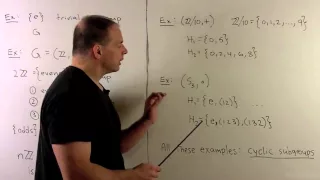Algebraic structures | Semigroup theory
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative internal binary operation on it. The binary operation of a semigroup is most often denoted multiplicatively: x·y, or simply xy, denotes the result of applying the semigroup operation to the ordered pair (x, y). Associativity is formally expressed as that (x·y)·z = x·(y·z) for all x, y and z in the semigroup. Semigroups may be considered a special case of magmas, where the operation is associative, or as a generalization of groups, without requiring the existence of an identity element or inverses. As in the case of groups or magmas, the semigroup operation need not be commutative, so x·y is not necessarily equal to y·x; a well-known example of an operation that is associative but non-commutative is matrix multiplication. If the semigroup operation is commutative, then the semigroup is called a commutative semigroup or (less often than in the analogous case of groups) it may be called an abelian semigroup. A monoid is an algebraic structure intermediate between semigroups and groups, and is a semigroup having an identity element, thus obeying all but one of the axioms of a group: existence of inverses is not required of a monoid. A natural example is strings with concatenation as the binary operation, and the empty string as the identity element. Restricting to non-empty strings gives an example of a semigroup that is not a monoid. Positive integers with addition form a commutative semigroup that is not a monoid, whereas the non-negative integers do form a monoid. A semigroup without an identity element can be easily turned into a monoid by just adding an identity element. Consequently, monoids are studied in the theory of semigroups rather than in group theory. Semigroups should not be confused with quasigroups, which are a generalization of groups in a different direction; the operation in a quasigroup need not be associative but quasigroups preserve from groups a notion of division. Division in semigroups (or in monoids) is not possible in general. The formal study of semigroups began in the early 20th century. Early results include a Cayley theorem for semigroups realizing any semigroup as transformation semigroup, in which arbitrary functions replace the role of bijections from group theory. A deep result in the classification of finite semigroups is Krohn–Rhodes theory, analogous to the Jordan–Hölder decomposition for finite groups. Some other techniques for studying semigroups, like Green's relations, do not resemble anything in group theory. The theory of finite semigroups has been of particular importance in theoretical computer science since the 1950s because of the natural link between finite semigroups and finite automata via the syntactic monoid. In probability theory, semigroups are associated with Markov processes. In other areas of applied mathematics, semigroups are fundamental models for linear time-invariant systems. In partial differential equations, a semigroup is associated to any equation whose spatial evolution is independent of time. There are numerous special classes of semigroups, semigroups with additional properties, which appear in particular applications. Some of these classes are even closer to groups by exhibiting some additional but not all properties of a group. Of these we mention: regular semigroups, orthodox semigroups, semigroups with involution, inverse semigroups and cancellative semigroups. There are also interesting classes of semigroups that do not contain any groups except the trivial group; examples of the latter kind are bands and their commutative subclass—semilattices, which are also ordered algebraic structures. (Wikipedia).