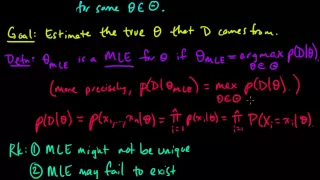Maximum likelihood estimation | Probability distribution fitting | M-estimators
Maximum likelihood estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed statistical model, the observed data is most probable. The point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when all observed outcomes are assumed to have Normal distributions with the same variance. From the perspective of Bayesian inference, MLE is generally equivalent to maximum a posteriori (MAP) estimation with uniform prior distributions (or a normal prior distribution with a standard deviation of infinity). In frequentist inference, MLE is a special case of an extremum estimator, with the objective function being the likelihood. (Wikipedia).