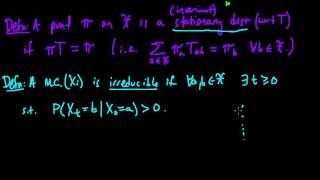Discrete-time Markov chain
In probability, a discrete-time Markov chain (DTMC) is a sequence of random variables, known as a stochastic process, in which the value of the next variable depends only on the value of the current variable, and not any variables in the past. For instance, a machine may have two states, A and E. When it is in state A, there is a 40% chance of it moving to state E and a 60% chance of it remaining in state A. When it is in state E, there is a 70% chance of it moving to A and a 30% chance of it staying in E. The sequence of states of the machine is a Markov chain. If we denote the chain by then is the state which the machine starts in and is the random variable describing its state after 10 transitions. The process continues forever, indexed by the natural numbers. An example of a stochastic process which is not a Markov chain is the model of a machine which has states A and E and moves to A from either state with 50% chance if it has ever visited A before, and 20% chance if it has never visited A before (leaving a 50% or 80% chance that the machine moves to E). This is because the behavior of the machine depends on the whole history—if the machine is in E, it may have a 50% or 20% chance of moving to A, depending on its past values. Hence, it does not have the Markov property. A Markov chain can be described by a stochastic matrix, which lists the probabilities of moving to each state from any individual state. From this matrix, the probability of being in a particular state n steps in the future can be calculated. A Markov chain's state space can be partitioned into communicating classes that describe which states are reachable from each other (in one transition or in many). Each state can be described as transient or recurrent, depending on the probability of the chain ever returning to that state. Markov chains can have properties including periodicity, reversibility and stationarity. A continuous-time Markov chain is like a discrete-time Markov chain, but it moves states continuously through time rather than as discrete time steps. Other stochastic processes can satisfy the Markov property, the property that past behavior does not affect the process, only the present state. (Wikipedia).