Combinatorial game theory
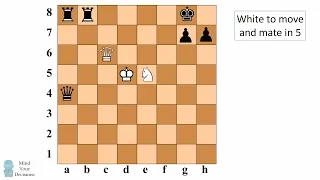
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Study has been largely confined to two-player games that have a position that the players take turns changing in defined ways or moves to achieve a defined winning condition. Combinatorial game theory has not traditionally studied games of chance or those that use imperfect or incomplete information, favoring games that offer perfect information in which the state of the game and the set of available moves is always known by both players. However, as mathematical techniques advance, the types of game that can be mathematically analyzed expands, thus the boundaries of the field are ever changing. Scholars will generally define what they mean by a "game" at the beginning of a paper, and these definitions often vary as they are specific to the game being analyzed and are not meant to represent the entire scope of the field. Combinatorial games include well-known games such as chess, checkers, and Go, which are regarded as non-trivial, and tic-tac-toe, which is considered as trivial, in the sense of being "easy to solve". Some combinatorial games may also have an unbounded playing area, such as infinite chess. In combinatorial game theory, the moves in these and other games are represented as a game tree. Combinatorial games also include one-player combinatorial puzzles such as Sudoku, and no-player automata, such as Conway's Game of Life, (although in the strictest definition, "games" can be said to require more than one participant, thus the designations of "puzzle" and "automata".) Game theory in general includes games of chance, games of imperfect knowledge, and games in which players can move simultaneously, and they tend to represent real-life decision making situations. Combinatorial game theory has a different emphasis than "traditional" or "economic" game theory, which was initially developed to study games with simple combinatorial structure, but with elements of chance (although it also considers sequential moves, see extensive-form game). Essentially, combinatorial game theory has contributed new methods for analyzing game trees, for example using surreal numbers, which are a subclass of all two-player perfect-information games. The type of games studied by combinatorial game theory is also of interest in artificial intelligence, particularly for automated planning and scheduling. In combinatorial game theory there has been less emphasis on refining practical search algorithms (such as the alpha–beta pruning heuristic included in most artificial intelligence textbooks), but more emphasis on descriptive theoretical results (such as measures of game complexity or proofs of optimal solution existence without necessarily specifying an algorithm, such as the strategy-stealing argument). An important notion in combinatorial game theory is that of the solved game. For example, tic-tac-toe is considered a solved game, as it can be proven that any game will result in a draw if both players play optimally. Deriving similar results for games with rich combinatorial structures is difficult. For instance, in 2007 it was announced that checkers has been weakly solved—optimal play by both sides also leads to a draw—but this result was a computer-assisted proof. Other real world games are mostly too complicated to allow complete analysis today, although the theory has had some recent successes in analyzing Go endgames. Applying combinatorial game theory to a position attempts to determine the optimum sequence of moves for both players until the game ends, and by doing so discover the optimum move in any position. In practice, this process is torturously difficult unless the game is very simple. It can be helpful to distinguish between combinatorial "mathgames" of interest primarily to mathematicians and scientists to ponder and solve, and combinatorial "playgames" of interest to the general population as a form of entertainment and competition. However, a number of games fall into both categories. Nim, for instance, is a playgame instrumental in the foundation of combinatorial game theory, and one of the first computerized games. Tic-tac-toe is still used to teach basic principles of game AI design to computer science students. (Wikipedia).