
Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics

Weil conjectures 4 Fermat hypersurfaces
This talk is part of a series on the Weil conjectures. We give a summary of Weil's paper where he introduced the Weil conjectures by calculating the zeta function of a Fermat hypersurface. We give an overview of how Weil expressed the number of points of a variety in terms of Gauss sums. T
From playlist Algebraic geometry: extra topics

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Étale Cohomology and the Weil conjectures - 8/20/2020
Introduction to the course; the Weil conjectures; curves; Serre's analogue
From playlist Étale cohomology and the Weil conjectures
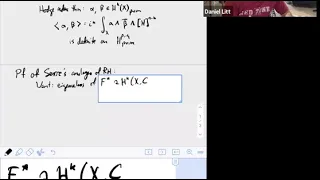
Étale cohomology Lecture II, 8/25/2020
Serre's complex analogue of the Riemann hypothesis, étale morphisms, intro to sites
From playlist Étale cohomology and the Weil conjectures

Weil conjectures 5: Lefschetz trace formula
This talk explains the relation between the Lefschetz fixed point formula and the Weil conjectures. More precisely, the zeta function of a variety of a finite field can be written in terms of an action of the Frobenius group on the cohomology groups of the variety. The main problem is then
From playlist Algebraic geometry: extra topics

“Gauss sums and the Weil Conjectures,” by Bin Zhao (Part 7 of 8)
“Gauss sums and the Weil Conjectures,” by Bin Zhao. The topics include will Gauss sums, Jacobi sums, and Weil’s original argument for diagonal hypersurfaces when he raised his conjectures. Further developments towards the Langlands program and the modularity theorem will be mentioned at th
From playlist CTNT 2016 - ``Gauss sums and the Weil Conjectures" by Bin Zhao

“Gauss sums and the Weil Conjectures,” by Bin Zhao (Part 4 of 8)
“Gauss sums and the Weil Conjectures,” by Bin Zhao. The topics include will Gauss sums, Jacobi sums, and Weil’s original argument for diagonal hypersurfaces when he raised his conjectures. Further developments towards the Langlands program and the modularity theorem will be mentioned at th
From playlist CTNT 2016 - ``Gauss sums and the Weil Conjectures" by Bin Zhao

Alvaro Lozano-Robledo, The distribution of ranks of elliptic curves and the minimalist conjecture
VaNTAGe seminar, on Sep 29, 2020 License: CC-BY-NC-SA. An updated version of the slides that corrects a few minor issues can be found at https://math.mit.edu/~drew/vantage/LozanoRobledoSlides.pdf
From playlist Math Talks

Christelle Vincent, Exploring angle rank using the LMFDB
VaNTAGe Seminar, February 15, 2022 License: CC-NC-BY-SA Links to some of the papers mentioned in the talk: Dupuy, Kedlaya, Roe, Vincent: https://arxiv.org/abs/2003.05380 Dupuy, Kedlaya, Zureick-Brown: https://arxiv.org/abs/2112.02455 Zarhin 1979: https://link.springer.com/article/10.100
From playlist Curves and abelian varieties over finite fields

David Corwin, Kim's conjecture and effective Faltings
VaNTAGe seminar, on Nov 24, 2020 License: CC-BY-NC-SA.
From playlist ICERM/AGNTC workshop updates

“Gauss sums and the Weil Conjectures,” by Bin Zhao (Part 5 of 8)
“Gauss sums and the Weil Conjectures,” by Bin Zhao. The topics include will Gauss sums, Jacobi sums, and Weil’s original argument for diagonal hypersurfaces when he raised his conjectures. Further developments towards the Langlands program and the modularity theorem will be mentioned at th
From playlist CTNT 2016 - ``Gauss sums and the Weil Conjectures" by Bin Zhao

The Biggest Project in Modern Mathematics
In a 1967 letter to the number theorist André Weil, a 30-year-old mathematician named Robert Langlands outlined striking conjectures that predicted a correspondence between two objects from completely different fields of math. The Langlands program was born. Today, it's one of the most amb
From playlist Explainers

Andrew Sutherland, Arithmetic L-functions and their Sato-Tate distributions
VaNTAGe seminar on April 28, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

“Gauss sums and the Weil Conjectures,” by Bin Zhao (Part 3 of 8)
“Gauss sums and the Weil Conjectures,” by Bin Zhao. The topics include will Gauss sums, Jacobi sums, and Weil’s original argument for diagonal hypersurfaces when he raised his conjectures. Further developments towards the Langlands program and the modularity theorem will be mentioned at th
From playlist CTNT 2016 - ``Gauss sums and the Weil Conjectures" by Bin Zhao

Math Park - 17/01/2015 - Olivier Wittenberg, De la topologie aux corps finis...
"De la topologie aux corps finis : autour des conjectures de Weil" Résumé : Les conjectures de Weil, énoncées à la fin des années 1940, constituèrent l'une des motivations principales pour le travail de Grothendieck en géométrie algébrique dans les années 1950 et 1960. Ces conjectures reli
From playlist Séminaire Mathematic Park
Valentijn Karemaker, Mass formulae for supersingular abelian varieties
VaNTAGe seminar, Jan 18, 2022 License: CC-BY-NC-SA Links to some of the papers mentioned in this talk: Oort: https://link.springer.com/chapter/10.1007/978-3-0348-8303-0_13 Honda: https://doi.org/10.2969/jmsj/02010083 Tate: https://link.springer.com/article/10.1007/BF01404549 Tate: https
From playlist Curves and abelian varieties over finite fields

Weil conjectures 2: Functional equation
This is the second lecture about the Weil conjectures. We show that the Riemann-Roch theorem implies the rationality and functional equation of the zeta function of a curve over a finite field.
From playlist Algebraic geometry: extra topics