Laplace's approximation

Statistical algorithms | Approximations

In mathematics, Laplace's approximation fits an un-normalised Gaussian approximation to a (twice differentiable) un-normalised target density. In Bayesian statistical inference this is useful to simultaneously approximate the posterior and the marginal likelihood, see also Approximate inference. The method works by matching the log density and curvature at a mode of the target density. For example, a (possibly non-linear) regression or classification model with data set comprising inputs and outputs has (unknown) parameter vector of length . The likelihood is denoted and the parameter prior . The joint density of outputs and parameters is the object of inferential desire The joint is equal to the product of the likelihood and the prior and by Bayes' rule, equal to the product of the marginal likelihood and posterior . Seen as a function of the joint is an un-normalised density. In Laplace's approximation we approximate the joint by an un-normalised Gaussian , where we use to denote approximate density, for un-normalised density and is a constant (independent of ). Since the marginal likelihood doesn't depend on the parameter and the posterior normalises over we can immediately identify them with and of our approximation, respectively. Laplace's approximation is where we have defined where is the location of a mode of the joint target density, also known as the maximum a posteriori or MAP point and is the positive definite matrix of second derivatives of the negative log joint target density at the mode . Thus, the Gaussian approximation matches the value and the curvature of the un-normalised target density at the mode. The value of is usually found using a gradient based method, e.g. Newton's method. In summary, we have for the approximate posterior over and the approximate log marginal likelihood respectively. In the special case of Bayesian linear regression with a Gaussian prior, the approximation is exact. The main weaknesses of Laplace's approximation are that it is symmetric around the mode and that it is very local: the entire approximation is derived from properties at a single point of the target density. Laplace's method is widely used and was pioneered in the context of neural networks by David MacKay and for Gaussian processes by Williams and Barber, see references. (Wikipedia).

Differential Equations | The Laplace Transform of a Derivative

We establish a formula involving the Laplace transform of the derivative of a function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/

From playlist The Laplace Transform

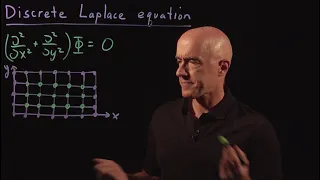
Discrete Laplace Equation | Lecture 62 | Numerical Methods for Engineers

Derivation of the discrete Laplace equation using the central difference approximations for the partial derivatives. Join me on Coursera: https://www.coursera.org/learn/numerical-methods-engineers Lecture notes at http://www.math.ust.hk/~machas/numerical-methods-for-engineers.pdf Subscr

From playlist Numerical Methods for Engineers

Introduction to Laplace Transforms

Introduction to Laplace Transforms A full introduction. The definition is given, remarks are made, and an example of finding the laplace transform of a function with the definition is done.

From playlist Differential Equations

C75 Introduction to the Laplace Transform

Another method of solving differential equations is by firs transforming the equation using the Laplace transform. It is a set of instructions, just like differential and integration. In fact, a function is multiplied by e to the power negative s times t and the improper integral from ze

From playlist Differential Equations

Differential Equations | Laplace Transform of a Piecewise Function

We find the Laplace transform of a piecewise function using the unit step function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/

From playlist The Laplace Transform

Approximation methods

A quick run over different approximation methods an why we would use them. The reference to the Skogestad method is to this video: https://youtu.be/pSG1FBxCvkE

From playlist Laplace

Laplace Equation Solutions

We see some examples of how we can use the properties of solutions to Laplace's Equation to "guess" solutions for the electric potential in some simple cases.

From playlist Phys 331 Uploads

Introduction to Laplace transforms

Free ebook https://bookboon.com/en/partial-differential-equations-ebook A basic introduction to the Laplace transform. We define it and show how to calculate Laplace transforms from the definition. We also discuss inverse transforms and how to use a table of transforms. Such ideas have

From playlist Partial differential equations

Laplace Derivation

Derivation of Laplace's Equation In this video, I derive Laplace's equation from first principles, staring with a fluid in equilibrium and using the divergence theorem. This derivation is particularly elegant and coordinate-free. Enjoy! Subscribe to my channel: https://www.youtube.com/c/

From playlist Partial Differential Equations

Introduction to linear analysis

Contrasting solving the exact equations approximately with solving the approximate equations exactly

From playlist Laplace

8ECM Invited Lecture: Nick Trefethen

From playlist 8ECM Invited Lectures

Lecture 23: Physically Based Animation and PDEs (CMU 15-462/662)

Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz2emSh0UQ5iOdT2xRHFHL7E Course information: http://15462.courses.cs.cmu.edu/

From playlist Computer Graphics (CMU 15-462/662)

Control of fluid motion by Mythily Ramaswamy

Program : Integrable systems in Mathematics, Condensed Matter and Statistical Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L

From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Lecture 18: The Laplace Operator (Discrete Differential Geometry)

Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg

From playlist Discrete Differential Geometry - CMU 15-458/858

Stirling's Incredible Approximation // Gamma Functions, Gaussians, and Laplace's Method

We prove Stirling's Formula that approximates n! using Laplace's Method. ►Get my favorite, free calculator app for your phone or tablet: MAPLE CALCULATOR: https://www.maplesoft.com/products/maplecalculator/download.aspx?p=TC-9857 ►Check out MAPLE LEARN for your browser to make beautiful gr

From playlist Cool Math Series

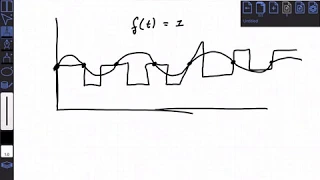
Inverting the Z transform and Z transform of systems

I move from signals to systems in describing discrete systems in the z domain

From playlist Discrete

Benjamin Stamm: A perturbation-method-based post-processing of planewave approximations for

Benjamin Stamm: A perturbation-method-based post-processing of planewave approximations for Density Functional Theory (DFT) models The lecture was held within the framework of the Hausdorff Trimester Program Multiscale Problems: Workshop on Non-local Material Models and Concurrent Multisc

From playlist HIM Lectures: Trimester Program "Multiscale Problems"

Differential Equations: Lecture 7.1 Definition of the Laplace Transform

This is a real classroom lecture on Differential Equations. I covered section 7.1 which is on the Definition of the Laplace Transform. I hope this video is helpful to someone. If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel

From playlist Differential Equations Full Lectures

Laplace's approximation

Related pages