
Milad Bakhshizadeh (Columbia) -- Sharp Concentration Resultsfor Heavy-Tailed Distributions
We obtain concentration and large deviation for the sums of independent and identically distributed random variables with heavy-tailed distributions. Our main theorem can not only recover some of the existing results, such as the concentration of the sum of subWeibull random variables, but
From playlist Northeastern Probability Seminar 2020
The Normal Distribution (1 of 3: Introductory definition)
More resources available at www.misterwootube.com
From playlist The Normal Distribution

What is a bimodal distribution? How to find out if data fits a bimodal.
From playlist Probability Distributions

Welcome to Quantitative Risk Management (QRM). There is so much confusion about tails, that it is time to clarify what we are speaking about. Heavy tails, long tails and fat tails are not the same thing from a statistical and probabilistic point of view. In mathematics we need to be preci
From playlist Quantitative Risk Management

What is a Unimodal Distribution?
Quick definition of a unimodal distribution and how it compares to a bimodal distribution and a multimodal distribution.
From playlist Probability Distributions

New: Two-Tailed Feature for All Distributions!
📣 Our probability calculator now has a two-tailed option for all distributions! 📣 https://www.geogebra.org/classic#probability
From playlist New Features and Releases

Multivariate Gaussian distributions
Properties of the multivariate Gaussian probability distribution
From playlist cs273a

Uniform Probability Distribution Examples
Overview and definition of a uniform probability distribution. Worked examples of how to find probabilities.
From playlist Probability Distributions

Is the Frequency Distribution Normal using a Strict Interpretation?
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Is the Frequency Distribution Normal using a Strict Interpretation?
From playlist Statistics

Kurtosis of a probability distribution (FRM T2-7)
[Here is my xls http://trtl.bz/121817-yt-kurtosis-xls] Kurtosis is the standardized fourth central moment and is a measure of tail density; e.g., heavy or fat-tails. Heavy-tailedness also tends to correspond to high peakedness. Excess kurtosis (aka, leptokurtosis) is given by (kurtosis-3).
From playlist Quantitative Analysis (FRM Topic 2)

This is the video of my talk at the Conference on Complex Systems 2020 (CCS2020), in the satellite event organised by Alfredo J. Morales (MIT) and Rosa M. Benito (Technical University of Madrid). For privacy reasons, I have cut the video, not to show the pictures of the other participants
From playlist Talks and Interviews

Environment oblivious risk-aware bandit algorithms by Jayakrishnan Nair
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

QRM 4-2: The Fisher-Tippett and the Pickands-Balkema-de Haan Theorems
Welcome to Quantitative Risk Management (QRM). It is time to discuss the two fundamental theorems of EVT. We will give the necessary information, for their interpretation and use, but we will skip the proofs. Most of all, we will try to connect the two theorems, which give us extremely st
From playlist Quantitative Risk Management

Thomas Mikosch : Asymptotic theory for the sample covariance matrix of a heavy-tailed [...]
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Probability and Statistics

Twitch Talks - Probability and Statistics
Presenter: Gosia Konwerska Wolfram Research developers demonstrate the new features of Version 12 of the Wolfram Language that they were responsible for creating. Previously broadcast live on June 6, 2019 at twitch.tv/wolfram. For more information, visit: https://www.wolfram.com/language/
From playlist Twitch Talks

12. Testing Goodness of Fit (cont.)
MIT 18.650 Statistics for Applications, Fall 2016 View the complete course: http://ocw.mit.edu/18-650F16 Instructor: Philippe Rigollet In this lecture, Prof. Rigollet talked about Kolmogorov-Lilliefors test, Quantile-Quantile plots, and Kai-squared goodness-of-fit test. License: Creative
From playlist MIT 18.650 Statistics for Applications, Fall 2016

Spectral Large Deviations for Sparse Random Matrices by Kyeongsik Nam
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

Distribution, Mean, Median, Mode, Range and Standard Deviation Lesson
This is part 1 of a lesson on describing data.
From playlist The Normal Distribution
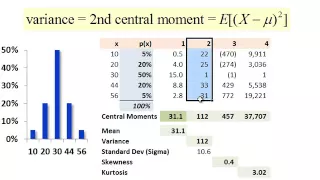
FRM: Distribution moments (mean, variance, skew, kurtosis)
Here is the spreadsheet I used @ http://db.tt/bziK312h. The four central moments of a distribution are mean (1st), variance, skew and kurtosis. They tell us quickly about the personality of the distribution. For more financial risk videos, visit our website! http://www.bionicturtle.com.
From playlist Operational Risk Analytics