In this video, I state and prove Chebyshev's inequality, and its cousin Markov's inequality. Those inequalities tell us how big an integrable function can really be. Enjoy!
From playlist Real Analysis

Statistics - How to use Chebyshev's Theorem
In this video I cover at little bit of what Chebyshev's theorem says, and how to use it. Remember that Chebyshev's theorem can be used with any distribution, and that it gives a lower proportion of what we can expect in the actual data. ▬▬ Chapters ▬▬▬▬▬▬▬▬▬▬▬ 0:00 Start 0:04 What is C
From playlist Statistics

Probability: Chebyshev's Inequality Proof & Example
Today, we prove Chebyshev's inequality and give an example.
From playlist Probability

CHEBYSHEV’S Theorem: An Inequality for Everyone (6-7)
Chebyshev’s Theorem (or Chebyshev’s Inequality) states that at least 1- (1/z2) of the items in any data set will be within z standard deviations of the mean, where z is any value greater than 1 and z need not be an integer. At least 75% of the data values must be within z = 2 standard dev
From playlist Depicting Distributions from Boxplots to z-Scores (WK 6 QBA 237)

How to solve Chebyshev's equation
I show how to solve Chebyshev's differential equation via an amazing substitution. The substitution results in forming a new differential equation with constant coefficients.
From playlist Differential equations

This statistics video tutorial provides a basic introduction into Chebyshev's theorem which states that the minimum percentage of distribution values that lie within k standard deviations of the mean is equal to 1 - 1/K^2. How To Calculate Federal Income Taxes: https://www.youtube.com/wat
From playlist Statistics

Algebra - Ch. 31: Linear Inequality in 2 Variables (2 of 14) Differences
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn the difference between “greater-than or equalto” and “greater-than”, and “less-than or equal to” and “less-than” graphi
From playlist ALGEBRA CH 31 LINEAR INEQUALITIES IN 2 VARIABLES

Thanks to all of you who support me on Patreon. You da real mvps! $1 per month helps!! :) https://www.patreon.com/patrickjmt !! Chebyshev's Theorem - In this video, I state Chebyshev's Theorem and use it in a 'real life' problem.
From playlist All Videos - Part 4

MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013 View the complete course: http://ocw.mit.edu/6-041SCF13 Instructor: Kuang Xu License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013

MIT RES.6-012 Introduction to Probability, Spring 2018 View the complete course: https://ocw.mit.edu/RES-6-012S18 Instructor: John Tsitsiklis License: Creative Commons BY-NC-SA More information at https://ocw.mit.edu/terms More courses at https://ocw.mit.edu
From playlist MIT RES.6-012 Introduction to Probability, Spring 2018

12/05/2019, Nicolas Brisebarre
Nicolas Brisebarre, École Normale Supérieure de Lyon Title: Correct rounding of transcendental functions: an approach via Euclidean lattices and approximation theory Abstract: On a computer, real numbers are usually represented by a finite set of numbers called floating-point numbers. Wh
From playlist Fall 2019 Symbolic-Numeric Computing Seminar

Ramon van Handel: The mysterious extremals of the Alexandrov-Fenchel inequality
The Alexandrov-Fenchel inequality is a far-reaching generalization of the classical isoperimetric inequality to arbitrary mixed volumes. It is one of the central results in convex geometry, and has deep connections with other areas of mathematics. The characterization of its extremal bodie
From playlist Trimester Seminar Series on the Interplay between High-Dimensional Geometry and Probability

MIT 6.041 Probabilistic Systems Analysis and Applied Probability, Fall 2010 View the complete course: http://ocw.mit.edu/6-041F10 Instructor: John Tsitsiklis License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013

Convergence in Probability and in the Mean Part 1
MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013 View the complete course: http://ocw.mit.edu/6-041SCF13 Instructor: Kuang Xu License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013

CTNT 2020 - Sieves (by Brandon Alberts) - Lecture 3
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Sieves (by Brandon Alberts)

Weird notions of "distance" || Intro to Metric Spaces
Visit https://brilliant.org/TreforBazett/ to get started learning STEM for free, and the first 200 people will get 20% off their annual premium subscription. Check out my MATH MERCH line in collaboration with Beautiful Equations ►https://www.beautifulequation.com/pages/trefor Weird, fun
From playlist Cool Math Series
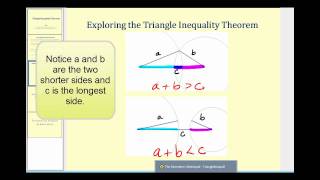
This video states and investigates the triangle inequality theorem. Complete Video List: http://www.mathispower4u.yolasite.com
From playlist Relationships with Triangles