
A short refresher on vectors. Before I introduce vector-based functions, it's important to look at vectors themselves and how they are represented in python™ and the IPython Notebook using SymPy.
From playlist Life Science Math: Vectors

Multivariable Calculus | The projection of a vector.
We define the projection of a vector in a certain direction. As an application we decompose a vector into the sum of a parallel and orthogonal component. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

This shows an small game that illustrates the concept of a vector. The clip is from the book "Immersive Linear Algebra" at http://www.immersivemath.com
From playlist Chapter 2 - Vectors
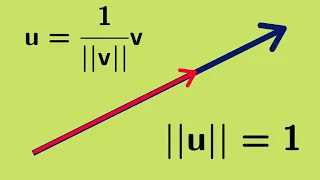
Multivariable Calculus | Unit Vectors
We define a unit vector, the unit basis vectors, and give some associated examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Vectors for Multivariable Calculus

http://www.freemathvideos.com In this video playlist I show you how to solve different math problems for Algebra, Geometry, Algebra 2 and Pre-Calculus. The video will provide you with math help using step by step instruction. Math help tutorials is just what you need for completing your
From playlist Vectors

What is the formula for the unit vector
http://www.freemathvideos.com In this video series I will show you how to find the unit vector when given a vector in component form and as a linear combination. A unit vector is simply a vector with the same direction but with a magnitude of 1 and an initial point at the origin. It is i
From playlist Vectors

Determining the Unit Tangent Vector
This video explains how to determine the unit tangent vector to a curve defined by a vector valued function. http://mathispower4u.wordpress.com/
From playlist Vectors

Calculus 3: Vector Calculus in 2D (23 of 39) What is the Unit Tangent Vector?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain and find the unit tangent vector T(t=2)=? of position vector r(t)=(t^2)i+3tj. Next video in the series can be seen at: https://youtu.be/c_YyUfD-NBw
From playlist CALCULUS 3 CH 3 VECTOR CALCULUS

Marc Levine: Refined enumerative geometry (Lecture 1)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Marc Levine: Refined enumerative geometry Abstract: Lecture 1: Milnor-Witt sheaves, motivic homotopy theory and Chow-Witt groups We review the Hoplins-Morel construction of the Miln
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

History of science 7: Did Witt discover the Leech lattice?
In about 1970 the German mathematician Witt claimed to have discovered the Leech lattice many years before Leech. This video explains what the Leech lattice is and examines the evidence for Witt's claim. Lieven Lebruyn discussed this question on his blog: http://www.neverendingbooks.org/w
From playlist History of science

Biring example: truncated lambda rings/witt vectors
Here we give the example of the biring that represents the functor of truncated witt vectors of length two.
From playlist Birings

This video explains how to find the unit vector of another vector given its components. The unit vector is equal to the vector divided by the magnitude of that vector. My Website: https://www.video-tutor.net Patreon Donations: https://www.patreon.com/MathScienceTutor Amazon Store: htt
From playlist New Precalculus Video Playlist

Yonatan Harpaz - New perspectives in hermitian K-theory I
For questions and discussions of the lecture please go to our discussion forum: https://www.uni-muenster.de/TopologyQA/index.php?qa=k%26l-conference This lecture is part of the event "New perspectives on K- and L-theory", 21-25 September 2020, hosted by Mathematics Münster: https://go.wwu
From playlist New perspectives on K- and L-theory

Marc Levine: Atiyah-Bott localization for Witt sheaf cohomology, with applications
30 September 2021 Abstract: Atiyah-Bott localization for singular cohomology of a space with a torus action has proven to be an effective tool in many areas, including enumerative geometry. We give here a parallel for cohomology with Witt-sheaf coeffcients, which is useful for computing q
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

Marc Levine: Refined enumerative geometry (Lecture 4)
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Lecture 4: Characteristic classes in Witt-cohomology Classical enumerative geometry relies heavily on the theory of Chern classes of vector bundles and the splitting principle, which
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Laurent Fargues - Courbes et fibrés vectoriels en théorie de Hodge p-adique
Courbes et fibrés vectoriels en théorie de Hodge p-adique
From playlist 28ème Journées Arithmétiques 2013

Replacing the ring A[t]/(t^2) with truncated witt vectors gives rise to derivative-like operations on the integers. This is the driving idea behind Buium's "Arithmetic Differential Equations" (they should be called wittferential equations!).
From playlist Witt Vectors/ Buium Geometry

Takeshi Saito - Upper ramification groups of local fields with imperfect residue fields (2/3)
Upper ramification groups of local fields with imperfect residue fields were introduced by two of the organizers, Abbes and myself in 2000. Recently the graded quotients are shown to be F_p-vector spaces and related to Frobenius-Witt differentials. In three lectures, we outline the definit
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)

Unit Vector in the Direction of v = (4, 7)
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Unit Vector in the Direction of v = (4, 7). We also check the answer.
From playlist Calculus

Takeshi Saito - Upper ramification groups of local fields with imperfect residue fields (3/3)
Upper ramification groups of local fields with imperfect residue fields were introduced by two of the organizers, Abbes and myself in 2000. Recently the graded quotients are shown to be F_p-vector spaces and related to Frobenius-Witt differentials. In three lectures, we outline the definit
From playlist Franco-Asian Summer School on Arithmetic Geometry (CIRM)