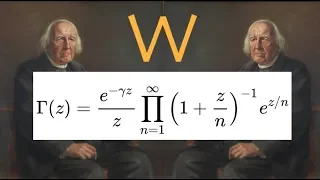
Infinite products & the Weierstrass factorization theorem
In this video we're going to explain the Weierstrass factorization theorem, giving rise to infinite product representations of functions. Classical examples are that of the Gamma function or the sine function. https://en.wikipedia.org/wiki/Weierstrass_factorization_theorem https://en.wiki
From playlist Programming
Math 139 Fourier Analysis Lecture 18: Weierstrass approximation; Heat Equation on the Line
Fourier transform and convolutions; Plancherel's theorem. Weierstrass approximation theorem. Application to PDEs: time-dependent heat equation on the line. The heat kernel. Convolution of a Schwartz-class function with the heat kernel solves the heat equation.
From playlist Course 8: Fourier Analysis

Bolzano-Weierstrass Theorem (Direct Proof) In this video, I present a more direct proof of the Bolzano-Weierstrass Theorem, that does not use any facts about monotone subsequences, and instead uses the definition of a supremum. This proof is taken from Real Mathematical Analysis by Pugh,
From playlist Sequences

Applying reimann sum for the midpoint rule and 3 partitions
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist The Integral

Weierstrass Polynomial Approximation Theorem
How can polynomials approximate continuous functions? I discuss the Weierstrass polynomial approximation theorem and provide a simple proof! This presentation is suitable for anyone who has a good understanding of a Calc 1 course. We use simple ideas like integration by parts and contin
From playlist Mathematical analysis and applications

Midpoint riemann sum approximation
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist The Integral

How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation
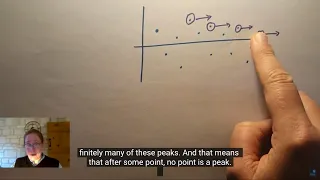
Analysis 1 - Convergent Subsequences: Oxford Mathematics 1st Year Student Lecture
This is the third lecture we're making available from Vicky Neale's Analysis 1 course for First Year Oxford Mathematics Students. Vicky writes: Does every sequence have a convergent subsequence? Definitely no, for example 1, 2, 3, 4, 5, 6, ... has no convergent subsequence. Does every b
From playlist Oxford Mathematics 1st Year Student Lectures

How to use midpoint rienmann sum with a table
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist The Integral

Commutative algebra 10 (Weierstrass preparation theorem)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we describe a second method of visualizing rings by drawing a point for each basis element of the ring. We giv
From playlist Commutative algebra

Short Proof of Bolzano-Weierstrass Theorem for Sequences | Real Analysis
Every bounded sequence has a convergent subsequence. This is the Bolzano-Weierstrass theorem for sequences, and we prove it in today's real analysis video lesson. We'll use two previous results that make this proof short and easy. First is the monotone subsequence theorem, stating that eve
From playlist Real Analysis

Real Analysis - Part 10 - Bolzano-Weierstrass theorem
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics Or via Patreon: https://www.patreon.com/bsom Or via other methods: https://thebrightsideofmathematics.
From playlist Real Analysis

Math 131 Fall 2018 120718 End of Stone Weierstrass
[Proof of Stone-Weierstrass theorem.] Recall method of approximation of the identity. Construction of polynomials. Proof: the standard trick (mass of kernel is 1); splitting trick. Uniform continuity of the function + uniform convergence of the kernels gives the necessary control.
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Real Analysis - Part 10 - Bolzano-Weierstrass theorem [dark version]
Support the channel on Steady: https://steadyhq.com/en/brightsideofmaths Or support me via PayPal: https://paypal.me/brightmaths Or via Ko-fi: https://ko-fi.com/thebrightsideofmathematics Or via Patreon: https://www.patreon.com/bsom Or via other methods: https://thebrightsideofmathematics.
From playlist Real Analysis [dark version]

Math 101 Fall 2017 Bolzano Weierstrass for Sequences
Theorem: any accumulation point of a sequence is a subsequential limit. Theorem: (Bolzano-Weierstrass) Any bounded sequence of real numbers has a convergent subsequence.
From playlist Course 6: Introduction to Analysis (Fall 2017)

For the latest information, please visit: http://www.wolfram.com Speaker: Paul Abbott When the eigenvalues of an operator A can be computed and form a discrete set, the spectral zeta function of A reduces to a sum over eigenvalues, when the sum exists. Belloni and Robinett used the “quan
From playlist Wolfram Technology Conference 2014

Multidimensional Bolzano Weierstraß
In this video, I prove the celebrated Bolzano-Weierstraß theorem in n dimensions, which says that a bounded sequence in R^n must have a convergent subsequence. This is the most important fact in analysis, and a lot of nice results follow from it Bolzano-Weierstraß: https://youtu.be/PapmU
From playlist Topology

The Bolzano Weierstraß Theorem
Bolzano-Weierstrass Theorem Welcome to one of the cornerstone theorems in Analysis: The Bolzano-Weierstraß Theorem. It is the culmination of all our hard work on monotone sequences, and we'll use this over and over again in this course. Luckily the proof isn't very difficult, since we've
From playlist Sequences
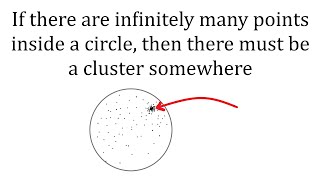
[#SoME1] A simple statement with a remarkable proof ( + Proof of Bolzano-Weierstrass Theorem)
In this video, I present a very important statement that, at first, seems quite obvious, but whose proof requires some neat reasoning. I start off by explaining everything required in order to understand the problem, and then restate it in a more rigorous way. Then, I present two proofs f
From playlist Summer of Math Exposition Youtube Videos