Vertex operator algebra

Non-associative algebra | Lie algebras

In mathematics, a vertex operator algebra (VOA) is an algebraic structure that plays an important role in two-dimensional conformal field theory and string theory. In addition to physical applications, vertex operator algebras have proven useful in purely mathematical contexts such as monstrous moonshine and the geometric Langlands correspondence. The related notion of vertex algebra was introduced by Richard Borcherds in 1986, motivated by a construction of an infinite-dimensional Lie algebra due to Igor Frenkel. In the course of this construction, one employs a Fock space that admits an action of vertex operators attached to lattice vectors. Borcherds formulated the notion of vertex algebra by axiomatizing the relations between the lattice vertex operators, producing an algebraic structure that allows one to construct new Lie algebras by following Frenkel's method. The notion of vertex operator algebra was introduced as a modification of the notion of vertex algebra, by Frenkel, James Lepowsky, and Arne Meurman in 1988, as part of their project to construct the moonshine module. They observed that many vertex algebras that appear in nature have a useful additional structure (an action of the Virasoro algebra), and satisfy a bounded-below property with respect to an energy operator. Motivated by this observation, they added the Virasoro action and bounded-below property as axioms. We now have post-hoc motivation for these notions from physics, together with several interpretations of the axioms that were not initially known. Physically, the vertex operators arising from holomorphic field insertions at points (i.e., vertices) in two-dimensional conformal field theory admit operator product expansions when insertions collide, and these satisfy precisely the relations specified in the definition of vertex operator algebra. Indeed, the axioms of a vertex operator algebra are a formal algebraic interpretation of what physicists call chiral algebras, or "algebras of chiral symmetries", where these symmetries describe the Ward identities satisfied by a given conformal field theory, including conformal invariance. Other formulations of the vertex algebra axioms include Borcherds's later work on singular commutative rings, algebras over certain operads on curves introduced by Huang, Kriz, and others, and D-module-theoretic objects called chiral algebras introduced by Alexander Beilinson and Vladimir Drinfeld. While related, these chiral algebras are not precisely the same as the objects with the same name that physicists use. Important basic examples of vertex operator algebras include lattice VOAs (modeling lattice conformal field theories), VOAs given by representations of affine Kac–Moody algebras (from the WZW model), the Virasoro VOAs (i.e., VOAs corresponding to representations of the Virasoro algebra) and the moonshine module V♮, which is distinguished by its monster symmetry. More sophisticated examples such as and the on a complex manifold arise in geometric representation theory and mathematical physics. (Wikipedia).

A gentle description of a vertex algebra.

Working from the notions of associative algebras, Lie algebras, and Poisson algebras we build the idea of a vertex algebra. We end with the proper definition as well as an "intuition" for how to think of the parts. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation

From playlist Vertex Operator Algebras

A commutative vertex algebra.

We look an example of the universal commutative vertex algebra with one generator. This provides a way of endowing a certain polynomial ring with the structure of a vertex algebra. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/

From playlist Vertex Operator Algebras

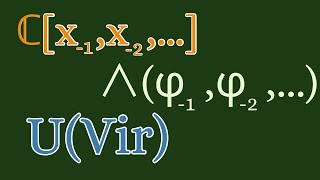
The vector spaces for vertex algebras.

We give some examples of the types of vector spaces it is important to be comfortable with in order to study vertex algebras. We look at three main example, a polynomial ring in infinitely many variables, the exterior algebra of infinitely many variables, and the universal enveloping algeb

From playlist Vertex Operator Algebras

The normally ordered product.

Along our way to understand the "internal" structure of a vertex algebra we look at the notion of the normally ordered product of two vertex operators and why we need such a definition. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.

From playlist Vertex Operator Algebras

Some reasons why vertex algebras are interesting.

We give some reasons why anyone would want to study vertex algebras. We include their connection to group theory, number theory, and mathematical physics. More VOAs on youtube: https://www.youtube.com/c/seandownes/playlists Please Subscribe: https://www.youtube.com/michaelpennmath?sub_co

From playlist Vertex Operator Algebras

The Heisenberg Algebra part 1.

We begin to describe the Heisenberg vertex algebra, which is an algebraic model of one free boson. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Website: http://www.michael-penn.net Randolph Col

From playlist Vertex Operator Algebras

Some example calculations in the Heisenberg vertex algebra.

We look at some examples of in depth calculations in the Heisenberg vertex algebra. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Website:

From playlist Vertex Operator Algebras

The Genesis of Vertex Algebras

We have a guest for this very special video. Richard Borcherds (Berkeley) has contributed a video regarding the history of vertex algebras. This video was also posted on his channel and is included here as well with permission and to increase its reach. Subscribe to his channel: https:/

From playlist Vertex Operator Algebras

Vertex Algebras | The non-negative products.

We examine some of the structure of the non-negative products of a vertex algebra. Vertex Algebra Books: Kac: https://amzn.to/2HsP2CK Lepowsky-Li: https://amzn.to/3kuN17y Gannon: https://amzn.to/37AdA7N Frenkel-BenZvi: https://amzn.to/31Csqa9 Please Subscribe: https://www.youtube.com/mi

From playlist Vertex Operator Algebras

Permutation Orbifolds of Vertex Operator Algebras

This is a recording of a talk I gave at the Illinois State University Algebra Seminar. Suggest a problem: https://forms.gle/ea7Pw7HcKePGB4my5 Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Merch: https://teespring.com/stores/michael-penn-math Personal Websi

From playlist Research Talks

Genesis of vertex algebras

This is a historical talk giving my recollections of how vertex algebras were discovered. It was requested by Michael Penn for his series of videos on vertex algebras https://www.youtube.com/playlist?list=PL22w63XsKjqyx2FFUywi_mz91Jtih52yX

From playlist Math talks

Miroslav Rapčak - Vertex Algebras for Divisors in Toric 3 - folds

From playlist Higher Structures in Holomorphic and Topological Field Theory

Emily Cliff: Hilbert Schemes Lecture 8

SMRI Seminar Series: 'Hilbert Schemes' Lecture 8 Heisenberg algebras, Fock space representations and vertex algebra structure Emily Cliff (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way t

From playlist SMRI Course: Hilbert Schemes

Vertex operator algebra

Related pages