Curvature (mathematics) | Riemannian geometry | Trace theory

Scalar curvature

In the mathematical field of Riemannian geometry, the scalar curvature (or the Ricci scalar) is a measure of the curvature of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the geometry of the metric near that point. It is defined by a complicated explicit formula in terms of partial derivatives of the metric components, although it is also characterized by the volume of infinitesimally small geodesic balls. In the context of the differential geometry of surfaces, the scalar curvature is twice the Gaussian curvature, and completely characterizes the curvature of a surface. In higher dimensions, however, the scalar curvature only represents one particular part of the Riemann curvature tensor. The definition of scalar curvature via partial derivatives is also valid in the more general setting of pseudo-Riemannian manifolds. This is significant in general relativity, where scalar curvature of a Lorentzian metric is one of the key terms in the Einstein field equations. Furthermore, this scalar curvature is the Lagrangian density for the Einstein–Hilbert action, the Euler–Lagrange equations of which are the Einstein field equations in vacuum. The geometry of Riemannian metrics with positive scalar curvature has been widely studied. On noncompact spaces, this is the context of the positive mass theorem proved by Richard Schoen and Shing-Tung Yau in the 1970s, and reproved soon after by Edward Witten with different techniques. Schoen and Yau, and independently Mikhael Gromov and Blaine Lawson, developed a number of fundamental results on the topology of closed manifolds supporting metrics of positive scalar curvature. In combination with their results, Grigori Perelman's construction of Ricci flow with surgery in 2003 provided a complete characterization of these topologies in the three-dimensional case. (Wikipedia).

Video thumbnail

Yuguang Shi - Quasi-local mass and geometry of scalar curvature

Quasi-local mass is a basic notion in General Relativity. Geometrically, it can be regarded as a geometric quantity of a boundary of a 3-dimensional compact Riemannian manifold. Usually, it is in terms of area and mean curvature of the boundary. It is interesting to see that some of quasi

From playlist Not Only Scalar Curvature Seminar

Video thumbnail

8.01x - Module 03.01 - What is a vector, what is a scalar.

What is a vector, what is a scalar.

From playlist 8.01x - MIT Help Sessions

Video thumbnail

Scalars and Vectors | Statics

https://goo.gl/e6wdj2 for more FREE video tutorials covering Engineering Mechanics (Statics & Dynamics) The objectives of this video are to review the scalar & vector concept and to do distinguish between scalars and vectors. First of all, the video gives definition of scalar & vector whe

From playlist SpoonFeedMe: Engineering Mechanics (Statics & Dynamics)

Video thumbnail

Physics 2 - Motion In One-Dimension (1 of 22) Definition

Visit http://ilectureonline.com for more math and science lectures! In this video I will explain the definition vector and the difference between a scalar and vector.

From playlist MOST POPULAR VIDEOS

Video thumbnail

Notions of Scalar Curvature - Mikhail Gromov

Emerging Topics Working Group Topic: Notions of Scalar Curvature Speaker: Mikhail Gromov Affiliation: IHES Date: October 16, 2018 For more video please visit http://video.ias.edu

From playlist Mathematics

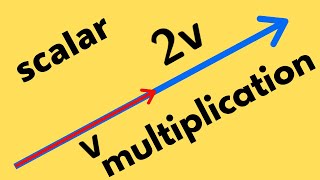
Video thumbnail

Multivariable Calculus | The scalar multiple of a vector.

We define scalar multiplication in the context of 2 and 3 dimensional vectors. We also present a few properties of scalar multiplication and vector addition. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/

From playlist Vectors for Multivariable Calculus

Video thumbnail

Scalars vs. Vectors

Describes the difference between scalars and vectors. You can see a listing of all my videos at my website, http://www.stepbystepscience.com

From playlist Motion Graphs; Position and Velocity vs. Time

Video thumbnail

Mikhail Gromov - Invitation to scalar curvature

There are three great domains in geometry, which lie on the boundary of "soft" and "rigid": (1) low dimensional, especially 4-dimensional topology/geometry; (2) symplectic topology/geometry; (3) scalar curvature bounded from below. I will try to elucidate in my lecture common fe

From playlist Not Only Scalar Curvature Seminar

Video thumbnail

What is General Relativity? Lesson 66: Scalar Curvature Part 15

What is General Relativity? Lesson 66: Scalar Curvature Part 15 We FINISH our examination of Section 4.4.6 of "A Simple Introduction to Particle Physics Part II - Geometric Foundations of Relativity." Here we finally learn how the scalar curvature can be interpreted as a correction to the

From playlist What is General Relativity?

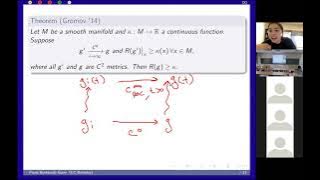
Video thumbnail

P. Burkhardt-Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow (vt)

We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second-order perturbation of the metric, that there exists a reasonable notion of a Ricci flow starti

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Video thumbnail

P. Burkhardt-Pointwise lower scalar curvature bounds for C0 metrics via regularizing Ricci flow

We propose a class of local definitions of weak lower scalar curvature bounds that is well defined for C0 metrics. We show the following: that our definitions are stable under greater-than-second-order perturbation of the metric, that there exists a reasonable notion of a Ricci flow starti

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

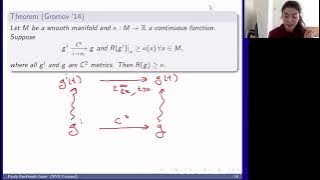
Video thumbnail

Paula Burkhardt-Guim - Lower scalar curvature bounds for $C^0$ metrics: a Ricci flow approach

We describe some recent work that has been done to generalize the notion of lower scalar curvature bounds to C^0 metrics, including a localized Ricci flow approach. In particular, we show the following: that there is a Ricci flow definition which is stable under greater-than-second-order p

From playlist Not Only Scalar Curvature Seminar

Video thumbnail

Bernhard Hanke - Surgery, bordism and scalar curvature

One of the most influential results in scalar curvature geometry, due to Gromov-Lawson and Schoen-Yau, is the construction of metrics with positive scalar curvature by surgery. Combined with powerful tools from geometric topology, this has strong implications for the classification of suc

From playlist Not Only Scalar Curvature Seminar

Video thumbnail

Rudolf Zeidler: Scalar curvature comparison via the Dirac operator

Talk by Rudolf Zeidler in Global Noncommutative Geometry Seminar (Americas) http://www.math.wustl.edu/~xtang/NCG-Seminar.html on September 23, 2020.

From playlist Global Noncommutative Geometry Seminar (Americas)

Video thumbnail

Rudolf Zeidler - Scalar and mean curvature comparison via the Dirac operator

I will explain a spinorial approach towards a comparison and rigidity principle involving scalar and mean curvature for certain warped products over intervals. This is motivated by recent scalar curvature comparison questions of Gromov, in particular distance estimates under lower scalar c

From playlist Talks of Mathematics Münster's reseachers

Video thumbnail

Chao Li: Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions

Talk by Chao Li in Global Noncommutative Geometry Seminar (Americas) on December 3, 2021. https://globalncgseminar.org/talks/tba-18/

From playlist Global Noncommutative Geometry Seminar (Americas)

Video thumbnail

Bifurcating conformal metrics with constant Q-curvature - Renato Bettiol

More videos on http://video.ias.edu

From playlist Variational Methods in Geometry

Video thumbnail

Claude LeBrun - Yamabe invariants, Weyl curvature, and the differential topology of 4-manifolds

The behavior of the Yamabe invariant, as defined in Bernd Ammann’s previous lecture, differs strangely in dimension 4 from what is seen in any other dimension. These peculiarities not only manifest themselves in the context of the usual scalar curvature, but also occur in connection with

From playlist Not Only Scalar Curvature Seminar

Video thumbnail

What is General Relativity? Lesson 52: Scalar Curvature Part I

What is General Relativity? Lesson 52: Scalar Curvature Part I This is the first of a few lectures about the Scalar Curvature and its interpretation. The goal is to get us to a point where we can have an interpretation of the Einstein Tensor and therefore an interpretation of the Einstein

From playlist What is General Relativity?

Video thumbnail

C. Li - Classifying sufficiently connected PSC manifolds in 4 and 5 dimensions (version temporaire)

In this talk, I will discuss some recent developments on the topology of closed manifolds admitting Riemannian metrics of positive scalar curvature. In particular, we will prove if a closed PSC manifold of dimension 4 (resp. 5) has vanishing π2 (resp. vanishing π2 and π3), then a finite co

From playlist Ecole d'été 2021 - Curvature Constraints and Spaces of Metrics

Related pages

Space form | Einstein manifold | Topology | Ricci decomposition | Holonomy | Weyl tensor | Partial derivative | Riemann curvature tensor | Maximum principle | Einstein tensor | Riemannian geometry | Closed manifold | Yamabe invariant | Connected sum | Friedmann–Lemaître–Robertson–Walker metric | Prescribed scalar curvature problem | Real number | Isometry | N-sphere | Fundamental group | Einstein–Hilbert action | Baum–Connes conjecture | Affine connection | Raising and lowering indices | Sectional curvature | Elliptic operator | Trace (linear algebra) | Atiyah–Singer index theorem | Hidehiko Yamabe | Torus | Christoffel symbols | Curvature of Riemannian manifolds | Dirac operator | Orthonormal frame | Vector bundle | Novikov conjecture | Ricci curvature | Einstein notation | Cobordism ring | Scalar curvature | Surgery theory | Gauss–Bonnet theorem | Euler characteristic | Hyperbolic space | Real projective space | Real projective plane | Riemannian manifold | Operator K-theory | Manifold | Einstein field equations | Principal curvature | Laplace–Beltrami operator | Gaussian curvature | Pseudo-Riemannian manifold | Calabi–Yau manifold | Thierry Aubin | Differential operator | Hyperboloid model | Differential geometry of surfaces | Kretschmann scalar | Schwarzschild metric | Schur's lemma (Riemannian geometry) | Ricci-flat manifold | Euler–Lagrange equation | Hyperkähler manifold | Normal coordinates | Constant curvature | Bertrand–Diguet–Puiseux theorem | Homothety | André Lichnerowicz | Minkowski space | K3 surface | Conformal geometry | Vermeil's theorem | Lagrangian (field theory) | Metric tensor | Exotic sphere | Invertible matrix | Pullback (differential geometry)