
Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Learn the basics for simplifying an expression using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule
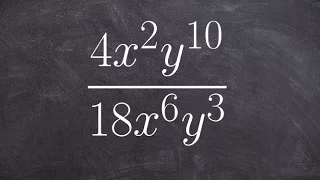
Simplify an expression by applying quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Learn how to simplify a monomial by applying quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule
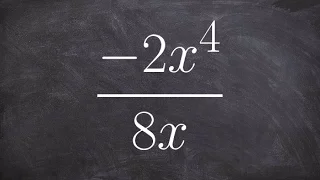
Simplifying a monomial using the rules of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Learn the basics in simplifying an expression using the quotient rule of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Simplifying an expression using properties of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Commutative algebra 24 Artinian modules
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We define Artinian rings and modules, and give several examples of them. We then study finite length modules, show that they
From playlist Commutative algebra

Kazhdan-Lusztig category - Jin-Cheng Guu
Quantum Groups Seminar Topic: Kazhdan-Lusztig category Speaker: Jin-Cheng Guu Affiliation: Stony Brook University Date: May 06, 2021 For more video please visit http://video.ias.edu
From playlist Quantum Groups Seminar

Lecture 15. Kernels and cokernels
From playlist Abstract Algebra 2

Lecture 17. Isomorphism theorems. Free modules
0:00 0:19 1st isomorphism theorem 1:15 2nd isomorphism theorem 4:56 3rd isomorphism theorem 9:40 Submodules of a quotient module 12:55 Generators 18:34 Finitely generated modules 30:21 Cautionary example: not every submodule of a finitely generated module is finitely generated 33:18 Linea
From playlist Abstract Algebra 2

The TRUTH about TENSORS, Part 3 The Tensoring
We finally start talking about the definition of tensors in terms of a universal property.
From playlist The TRUTH about TENSORS

Eugen Hellmann: On the derived category of the Iwahori-Hecke algebra
SMRI Algebra and Geometry Online 'On the derived category of the Iwahori-Hecke algebra' Eugen Hellmann (University of Münster) Abstract: In this talk I will state a conjecture which predicts that the derived category of smooth representations of a p-adic split reductive group admits a ful
From playlist SMRI Algebra and Geometry Online

Proof: Structure Theorem for Finitely Generated Torsion Modules Over a PID
This video has chapters to make the proof easier to follow. Splitting explanation: https://youtu.be/ZINtBNje_08 In this video we give a proof of the classification theorem using two smaller proofs by induction. We show both the elementary divisor form and the invariant factor form of a m
From playlist Ring & Module Theory

Gregory Henselman-Petrusek (9/28/22): Saecular persistence
Homology with field coefficients has become a mainstay of modern TDA, thanks in part to structure theorems which decompose the corresponding persistence modules. This naturally begs the question -- what of integer coefficients? Or homotopy? We introduce saecular persistence, a categoric
From playlist AATRN 2022

Nakayama's Lemma - April 12 2021
This is a video from by Abstract Algebra 4 course that took place in Spring 2021.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]

Simplify a rational expression by using properties of exponents
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Commutative algebra 27 (Associated primes)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We show that every finitely generated module M over a Noetherian ring R can broken up into modules of the form R/p for p prime
From playlist Commutative algebra