
When do fractional differential equations have solutions bounded by the Mittag-Leffler function?
When do fractional differential equations have solutions bounded by the Mittag Leffler function? New research into this question! http://www.degruyter.com/view/j/fca.2015.18.issue-3/fca-2015-0039/fca-2015-0039.xml?format=INT Fract. Calc. Appl. Anal. 18, no. 3 (2015), 642-650. DOI: 10.15
From playlist Mathematical analysis and applications

Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra
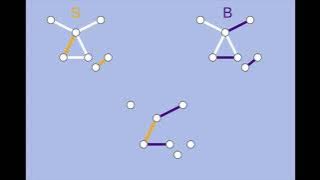
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

I define one of the most important constants in mathematics, the Euler-Mascheroni constant. It intuitively measures how far off the harmonic series 1 + 1/2 + ... + 1/n is from ln(n). In this video, I show that the constant must exist. It is an open problem to figure out if the constant is
From playlist Series

Banach fixed point theorem & differential equations
A novel application of Banach's fixed point theorem to fractional differential equations of arbitrary order. The idea involves a new metric based on the Mittag-Leffler function. The technique is applied to gain the existence and uniqueness of solutions to initial value problems. http://
From playlist Mathematical analysis and applications

This lecture is part of an online course on rings and modules. We discuss when taking limits of modules preserves exactness. In particular we give the Mittag-Leffler condition that ensures that taking inverse limits of modules preserves exactness. For the other lectures in the course see
From playlist Rings and modules

Gronwall's inequality & fractional differential equations
Several general versions of Gronwall's inequality are presented and applied to fractional differential equations of arbitrary order. Applications include: yielding a priori bounds and nonumultiplicity of solutions. This presentation features new mathematical research. http://projecteucli
From playlist Mathematical analysis and applications

In this video, I prove the famous Riemann-Lebesgue lemma, which states that the Fourier transform of an integrable function must go to 0 as |z| goes to infinity. This is one of the results where the proof is more important than the theorem, because it's a very classical Lebesgue integral
From playlist Real Analysis

Commutative algebra 48: Limits and exactness
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We discuss when the limit of exact sequences is exact. We show this happens whenever the "Mittag-Leffler condition" is satisfi
From playlist Commutative algebra

The Cotangent's Series Expansion Derivation using FOURIER SERIES [ Mittag-Leffler Theorem ]
Help me create more free content! =) https://www.patreon.com/mathable Merch :v - https://teespring.com/de/stores/papaflammy https://shop.spreadshirt.de/papaflammy 2nd Channel: https://www.youtube.com/channel/UCPctvztDTC3qYa2amc8eTrg Sine Product: https://youtu.be/G5foI
From playlist Fourier Series

Hermitian and Non-Hermitian Laplacians and Wave Equaions by Andrey shafarevich
Non-Hermitian Physics - PHHQP XVIII DATE: 04 June 2018 to 13 June 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore Non-Hermitian Physics-"Pseudo-Hermitian Hamiltonians in Quantum Physics (PHHQP) XVIII" is the 18th meeting in the series that is being held over the years in Quantum Phys
From playlist Non-Hermitian Physics - PHHQP XVIII

Here I prove the Heine-Borel Theorem, one of the most fundamental theorems in analysis. It says that in R^n, all boxes must be compact. The proof itself is very neat, and uses a bisection-type argument. Enjoy! Topology Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmA13vj9xkHG
From playlist Topology

Background material on the Cauchy-Riemann equations (Lecture 1) by Debraj Chakrabarti
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Chapter 3: Lagrange's theorem, Subgroups and Cosets | Essence of Group Theory
Lagrange's theorem is another very important theorem in group theory, and is very intuitive once you see it the right way, like what is presented here. This video also discusses the idea of subgroups and cosets, which are crucial in the development of the Lagrange's theorem. Other than c
From playlist Essence of Group Theory

Lennart Carleson - The Abel Prize interview 2006
0:00 Glimpses of the Abel Prize ceremony made for Norwegian television 05:00 Interview proper starts (Norwegian) 07:46 (English) Almost-everywhere convergence of Fourier series for square-integrable (L^2) functions 10:08 Interesting example of need to have conviction about outcome before c
From playlist The Abel Prize Interviews

Proof & Explanation: Gauss's Lemma in Number Theory
Euler's criterion: https://youtu.be/2IBPOI43jek One common proof of quadratic reciprocity uses Gauss's lemma. To understand Gauss's lemma, here we prove how it works using Euler's criterion and the Legendre symbol. Quadratic Residues playlist: https://www.youtube.com/playlist?list=PLug5Z
From playlist Quadratic Residues

This lecture is part of an online course on rings and modules. We continue the previous lecture on complete rings by discussing Hensel's lemma for finding roots of polynomials over p-adic rings or over power series rings. We sketch two proofs, by slowly improving a root one digit at a tim
From playlist Rings and modules

We finally get to Lagrange's theorem for finite groups. If this is the first video you see, rather start at https://www.youtube.com/watch?v=F7OgJi6o9po&t=6s In this video I show you how the set that makes up a group can be partitioned by a subgroup and its cosets. I also take a look at
From playlist Abstract algebra

This talk is the first of two talks that give a proof of the Riemann Roch theorem, in the spacial case of nonsingular complex plane curves. We divide the Riemann-Roch theorem into 3 pieces: Riemann's theorem, a topological theorem identifying the three definitions of the genus, and Roch'
From playlist Algebraic geometry: extra topics