Minimum degree algorithm

Matrix theory | Numerical linear algebra

In numerical analysis, the minimum degree algorithm is an algorithm used to permute the rows and columns of a symmetric sparse matrix before applying the Cholesky decomposition, to reduce the number of non-zeros in the Cholesky factor.This results in reduced storage requirements and means that the Cholesky factor can be applied with fewer arithmetic operations. (Sometimes it may also pertain to an incomplete Cholesky factor used as a preconditioner—for example, in the preconditioned conjugate gradient algorithm.) Minimum degree algorithms are often used in the finite element method where the reordering of nodes can be carried out depending only on the topology of the mesh, rather than on the coefficients in the partial differential equation, resulting in efficiency savings when the same mesh is used for a variety of coefficient values. Given a linear system where A is an real symmetric sparse square matrix. The Cholesky factor L will typically suffer 'fill in', that is have more non-zeros than the upper triangle of A. We seek a permutation matrix P, so that the matrix, which is also symmetric, has the least possible fill in its Cholesky factor. We solve the reordered system The problem of finding the best ordering is an NP-complete problem and is thus intractable, so heuristic methods are used instead. The minimum degree algorithm is derived from a method first proposed by Markowitz in 1959 for non-symmetric linear programming problems, which is loosely described as follows. At each step in Gaussian elimination row and column permutations are performed so as to minimize the number of off diagonal non-zeros in the pivot row and column. A symmetric versionof Markowitz method was described by Tinney and Walker in 1967 and Rose later derived a graph theoretic version of the algorithm where the factorization is only simulated, and this was named the minimum degree algorithm. The graph referred to is the graph with n vertices, with vertices i and j connected by an edge when , and the degree is the degree of the vertices. A crucial aspect of such algorithms is a tie breaking strategy when there is a choice of renumbering resulting in the same degree. A version of the minimum degree algorithm was implemented in the MATLAB function symmmd (where MMD stands for multiple minimum degree), but has now been superseded by a symmetric approximate multiple minimum degree function symamd, which is faster. This is confirmed by theoretical analysis, which shows that for graphs with n vertices and m edges, MMD has a tight upper bound of on its running time, whereas for AMD a tight bound of holds. Cummings, Fahrbach, and Fatehpuria designed an exact minimum degree algorithm with running time, and showed that no such algorithm can exist that runs in time , for any , assuming the strong exponential time hypothesis. (Wikipedia).

Bound on the Sum of Minimum Degrees of Graphs and their Complements | Graph Theory Proofs

We know the degree of a vertex in a simple graph with n vertices has an upper bound of n-1. The degree of a vertex is n-1 when it is adjacent to every vertex in the graph except for itself (it cannot be adjacent to itself). Then certainly the minimum degree of a graph is less than or equal

From playlist Graph Theory

Calculus: Absolute Maximum and Minimum Values

In this video, we discuss how to find the absolute maximum and minimum values of a function on a closed interval.

From playlist Calculus

Minimum and Maximum Degree Vertices in Complement Graphs | Graph Complements, Graph Theory

How do we know what vertices will have the minimum and maximum degree of a complement graph based on the degrees of the original graph? We go over properties about just this topic in today's video graph theory lesson! Let G be a graph with vertices v and u such that the degree of v is the

From playlist Graph Theory

Maximum and Minimum Values (Closed interval method)

A review of techniques for finding local and absolute extremes, including an application of the closed interval method

From playlist 241Fall13Ex3

Absolute Maximum and Minimum Values of a Function - Calculus I

This video teaches students how to use the closed interval test to find absolute maximum and minimum values of a function. In particular, I use the first derivative to find critical values of the function. From this step, I show how to find the absolute maximum and minimum values within

From playlist Calculus 1

Vertex Connectivity is Less than or Equal to Minimum Degree | Graph Theory Exercises

The vertex connectivity of every graph is less than or equal to its minimum degree, this is a simple upper bound on vertex connectivity. We prove this fact, and show an example, in today's graph theory video lesson. This inequality is true because if a graph G is disconnected, then its v

From playlist Graph Theory Exercises

2 2 Computing Minimum Edit Distance 5 54

From playlist CS124 - Full Course

2.2 Relative Maximum and Minimum

MATH 1314 Kilgore College

From playlist MATH 1314: College Algebra (depreciated)

CSE 373 -- Lecture 13, Fall 2020

From playlist CSE 373 -- Fall 2020

Анализ Социальных Сетей. Лекция 8. Разбиение графов

Слайды: http://www.leonidzhukov.net/hse/2014/socialnetworks/lectures/lecture8.pdf Aлгоритмы аппроксимации. Задача нахождения минимально разреза в графе. Алгори tм randomized min-cut. Многоуровневый подход. Нахождение сообществ многоурвневым методом. Локальная кластеризация. Понятие провод

From playlist Анализ Социальных Сетей. Курс НИУ ВШЭ

CSE 373 --- Lecture 13: Minimum Spanning Trees (Fall 2021)

10/7/21

From playlist CSE373 --- Analysis of Algorithms (Fall 2021)

CSE373 2012 - Lecture 14 - Graph Algorithms (con't)

This is Lecture 14 of the CSE373 (Analysis of Algorithms) course taught by Professor Steven Skiena [http://www.cs.sunysb.edu/~skiena/] at Stony Brook University in 2012.

From playlist CSE373 - Analysis of Algorithms - 2012 SBU

Pre-Calculus - Identify the local maximum and minimum of a function

This video shows how to find the local maximum and minimum points when looking at the graph of a function. Remember that these are the maximum and minimum on some interval of the entire function. More specific techniques are covered for other functions like quadratics in later videos. F

From playlist Pre-Calculus

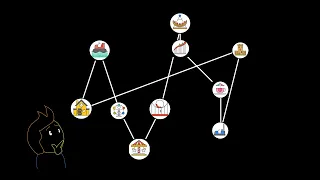
riding every amusement park ride in the shortest possible time

#SoME2 #maths #computerscience Have you ever wanted to optimize your route through an amusement park so that you hit every single ride in the shortest time possible? In this video we go over a famous problem in optimization in mathematics and computer science, the Traveling Salesman Pro

From playlist Summer of Math Exposition 2 videos

Lecture 13 - Minimum Spanning Trees I

This is Lecture 13 of the CSE373 (Analysis of Algorithms) course taught by Professor Steven Skiena [http://www3.cs.stonybrook.edu/~skiena/] at Stony Brook University in 2016. The lecture slides are available at: https://www.cs.stonybrook.edu/~skiena/373/newlectures/lecture13.pdf More inf

From playlist CSE373 - Analysis of Algorithms 2016 SBU

R9. Approximation Algorithms: Traveling Salesman Problem

MIT 6.046J Design and Analysis of Algorithms, Spring 2015 View the complete course: http://ocw.mit.edu/6-046JS15 Instructor: Amartya Shankha Biswas In this recitation, problems related to approximation algorithms are discussed, namely the traveling salesman problem. License: Creative Com

From playlist MIT 6.046J Design and Analysis of Algorithms, Spring 2015

Lecture 7. Graph partitioning algorithms.

Network Science 2021 @ HSE http://www.leonidzhukov.net/hse/2021/networks/

From playlist Network Science, 2021

Factorization-based Sparse Solvers and Preconditions, Lecture 3

Xiaoye Sherry Li's (from Lawrence Berkeley National Laboratory) lecture number three on Factorization-based sparse solves and preconditioners

From playlist Gene Golub SIAM Summer School Videos

#16. Find the Relative Minimum from the Graph

From playlist College Algebra Final Exam Playlist (Version 2)

9 4 Analysis of Contraction Algorithm 30 min

From playlist Algorithms 1

Minimum degree algorithm

Related pages