
Abstract Algebra | Irreducibles and Primes in Integral Domains
We define the notion of an irreducible element and a prime element in the context of an arbitrary integral domain. Further, we give examples of irreducible elements that are not prime. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://
From playlist Abstract Algebra

Abstract Algebra | Irreducible polynomials
We introduce the notion of an irreducible polynomial over the ring k[x] where k is any field. A proof that p(x) is irreducible if and only if (p(x)) is maximal is also given, along with some examples. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal W
From playlist Abstract Algebra

In this video I discuss irreducible polynomials and tests for irreducibility. Note that this video is intended for students in abstract algebra and is not appropriate for high-school or early college level algebra courses.
From playlist Abstract Algebra

Alina Ostafe: Dynamical irreducibility of polynomials modulo primes
Abstract: In this talk we look at polynomials having the property that all compositional iterates are irreducible, which we call dynamical irreducible. After surveying some previous results (mostly over finite fields), we will concentrate on the question of the dynamical irreducibility of
From playlist Number Theory Down Under 9

RT8.2. Finite Groups: Classification of Irreducibles
Representation Theory: Using the Schur orthogonality relations, we obtain an orthonormal basis of L^2(G) using matrix coefficients of irreducible representations. This shows the sum of squares of dimensions of irreducibles equals |G|. We also obtain an orthonormal basis of Class(G) usin
From playlist Representation Theory

Irreducibility (Eisenstein's Irreducibility Criterion)
Given a polynomial with integer coefficients, we can determine whether it's irreducible over the rationals using Eisenstein's Irreducibility Criterion. Unlike some our other technique, this works for polynomials of high degree! The tradeoff is that it works over the rationals, but need not
From playlist Modern Algebra - Chapter 11

Field Theory: Irreducible Polynomials
This video is about irreducible polynomials.
From playlist Basics: Field Theory

RNT2.2. Principal Ideal Domains
Ring Theory: We define PIDs and UFDs and describe their relationship. Prime and irreducible elements are defined, and conditions for implication are given. (second version: corrections to definition of prime and irreducible; comment should be 'R UFD implies R[x] UFD, improved proof that
From playlist Abstract Algebra

Rings and modules 4 Unique factorization
This lecture is part of an online course on rings and modules. We discuss unique factorization in rings, showing the implications (Integers) implies (Euclidean domain) implies (Principal ideal domain) implies (Unique factorization domain). We give a few examples to illustrate these implic
From playlist Rings and modules

Schemes 14: Irreducible, reduced, integral, connected
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We discuss the 4 properties of schemes: reduced, irreducible, integral, and connected.
From playlist Algebraic geometry II: Schemes

Visual Group Theory: Lecture 7.4: Divisibility and factorization
Visual Group Theory: Lecture 7.4: Divisibility and factorization The ring of integers have a number of properties that we take for granted: every number can be factored uniquely into primes, and all pairs of numbers have a unique gcd and lcm. In this lecture, we investigate when this happ
From playlist Visual Group Theory
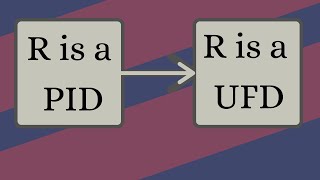
Abstract Algebra | Every PID is a UFD.
We prove the classical result in commutative algebra that every principal ideal domain is in fact a unique factorization domain. Along the way, we introduce the ascending chain condition and the notion of a Noetherian ring. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_co
From playlist Abstract Algebra

Commutative algebra 15 (Noetherian spaces)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we define Noetherian topological spaces, and use them to show that for a Noetherian ring R, every closed subse
From playlist Commutative algebra

Commutative algebra 14 (Irreducible subsets of Spec R)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we show that the irreducible closed subsets of Spec R are just the closures of points. We do this using the
From playlist Commutative algebra

Unique Factorization - Feb 08, 2021 - Rings and Modules
We introduce the Noetherianity hypothesis on rings and show that under this hypothesis that one can factor elements into a product of irreducible elements.
From playlist Course on Rings and Modules (Abstract Algebra 4) [Graduate Course]
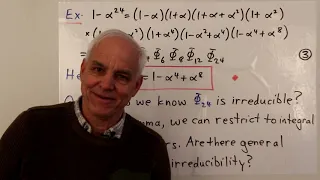
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

