Irreducibility (mathematics)

Mathematical terminology

In mathematics, the concept of irreducibility is used in several ways. * A polynomial over a field may be an irreducible polynomial if it cannot be factored over that field. * In abstract algebra, irreducible can be an abbreviation for irreducible element of an integral domain; for example an irreducible polynomial. * In representation theory, an irreducible representation is a nontrivial representation with no nontrivial proper subrepresentations. Similarly, an irreducible module is another name for a simple module. * Absolutely irreducible is a term applied to mean irreducible, even after any finite extension of the field of coefficients. It applies in various situations, for example to irreducibility of a linear representation, or of an algebraic variety; where it means just the same as irreducible over an algebraic closure. * In commutative algebra, a commutative ring R is irreducible if its prime spectrum, that is, the topological space Spec R, is an irreducible topological space. * A matrix is irreducible if it is not similar via a permutation to a block upper triangular matrix (that has more than one block of positive size). (Replacing non-zero entries in the matrix by one, and viewing the matrix as the adjacency matrix of a directed graph, the matrix is irreducible if and only if such directed graph is strongly connected.) A detailed definition is given here. * Also, a Markov chain is irreducible if there is a non-zero probability of transitioning (even if in more than one step) from any state to any other state. * In the theory of manifolds, an n-manifold is irreducible if any embedded (n − 1)-sphere bounds an embedded n-ball. Implicit in this definition is the use of a suitable category, such as the category of differentiable manifolds or the category of piecewise-linear manifolds. The notions of irreducibility in algebra and manifold theory are related. An n-manifold is called prime, if it cannot be written as a connected sum of two n-manifolds (neither of which is an n-sphere). An irreducible manifold is thus prime, although the converse does not hold. From an algebraist's perspective, prime manifolds should be called "irreducible"; however, the topologist (in particular the 3-manifold topologist) finds the definition above more useful. The only compact, connected 3-manifolds that are prime but not irreducible are the trivial 2-sphere bundle over S1 and the twisted 2-sphere bundle over S1. See, for example, Prime decomposition (3-manifold). * A topological space is irreducible if it is not the union of two proper closed subsets. This notion is used in algebraic geometry, where spaces are equipped with the Zariski topology; it is not of much significance for Hausdorff spaces. See also irreducible component, algebraic variety. * In universal algebra, irreducible can refer to the inability to represent an algebraic structure as a composition of simpler structures using a product construction; for example subdirectly irreducible. * A 3-manifold is P²-irreducible if it is irreducible and contains no 2-sided (real projective plane). * An irreducible fraction (or fraction in lowest terms) is a vulgar fraction in which the numerator and denominator are smaller than those in any other equivalent fraction.This article includes a list of related items that share the same name (or similar names). If an internal link incorrectly led you here, you may wish to change the link to point directly to the intended article. (Wikipedia).

Alina Ostafe: Dynamical irreducibility of polynomials modulo primes

Abstract: In this talk we look at polynomials having the property that all compositional iterates are irreducible, which we call dynamical irreducible. After surveying some previous results (mostly over finite fields), we will concentrate on the question of the dynamical irreducibility of

From playlist Number Theory Down Under 9

Irreducible Polynomials

In this video I discuss irreducible polynomials and tests for irreducibility. Note that this video is intended for students in abstract algebra and is not appropriate for high-school or early college level algebra courses.

From playlist Abstract Algebra

Irreducibility (Eisenstein's Irreducibility Criterion)

Given a polynomial with integer coefficients, we can determine whether it's irreducible over the rationals using Eisenstein's Irreducibility Criterion. Unlike some our other technique, this works for polynomials of high degree! The tradeoff is that it works over the rationals, but need not

From playlist Modern Algebra - Chapter 11

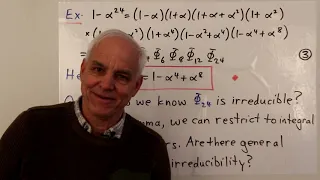
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger

In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some

From playlist Famous Math Problems

Lecture 7. Irreducibility and primeness. UFDs

From playlist Abstract Algebra 2

Unpredictability, Undecidability, and Uncomputability

Quite a number of mathematical theorems prove that the power of mathematics has its limits. But how relevant are these theorems for science? In this video I want to briefly summarize an essay that I just submitted to the essay contest of the Foundational Questions Institute. This year the

From playlist Philosophy of Science

Abstract Algebra | Irreducibles and Primes in Integral Domains

We define the notion of an irreducible element and a prime element in the context of an arbitrary integral domain. Further, we give examples of irreducible elements that are not prime. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://

From playlist Abstract Algebra

Abstract Algebra | Irreducible polynomials

We introduce the notion of an irreducible polynomial over the ring k[x] where k is any field. A proof that p(x) is irreducible if and only if (p(x)) is maximal is also given, along with some examples. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal W

From playlist Abstract Algebra

Divisibility, Prime Numbers, and Prime Factorization

Now that we understand division, we can talk about divisibility. A number is divisible by another if their quotient is a whole number. The smaller number is a factor of the larger one, but are there numbers with no factors at all? There's some pretty surprising stuff in this one! Watch th

From playlist Mathematics (All Of It)

Representation Theory(Repn Th) 2 by Gerhard Hiss

DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra

From playlist Group Theory and Computational Methods

What We've Learned from NKS Chapter 12: The Principle of Computational Equivalence [Part 1]

In this episode of "What We've Learned from NKS", Stephen Wolfram is counting down to the 20th anniversary of A New Kind of Science with [another] chapter retrospective. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or th

From playlist Science and Research Livestreams

The S3 character table - a (somewhat) new meaning | Diffusion Symmetry 2 | N J Wildberger

With diffusion symmetry, we explore mathematical objects or physical systems by spreading or diffusing from an initial point. The algebraic objects that result are hypergroups, or fusion algebra, or one of many similar and almost equivalent systems found in combinatorics, group theory, num

From playlist Diffusion Symmetry: A bridge between mathematics and physics

Algorithmic Construction of Representations of Finite Solvable Groups by Ravi S Kulkarni

From playlist Group Theory and Computational Methods

Wolfram Science Initiatives Update (September 15, 2022)

Join Stephen Wolfram as he discusses updates on the Physics Project, the Ruliad, Multicomputation, and Metamathematics! If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube channel or through the official Twitch channel of Stephen Wolfr

From playlist Science and Research Livestreams

Representation Theory(Repn Th) 1 by Gerhard Hiss

From playlist Group Theory and Computational Methods

What We've Learned from NKS 20 Years Later: The Making and Current State of NKS [Part 3]

In this episode of "What We've Learned from NKS", Stephen Wolfram is celebrating the 20th anniversary of A New Kind of Science with a look at the making of and current state of NKS. If you'd like to contribute to the discussion in future episodes, you can participate through this YouTube c

From playlist Science and Research Livestreams

Wolfram Summer School Physics Track Opening Keynote

Stephen wolfram gives his opening keynote for the Wolfram Summer School physics track. Find more information about the summer school here: https://education.wolfram.com/summer/school/ Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announceme

From playlist Wolfram Physics Project Livestream Archive

Nonlinear algebra, Lecture 9: "Representation Theory", by Mateusz Michalek

This is the ninth lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.

From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Pierre Emmanuel Caprace - Groups with irreducibly unfaithful subsets for unitary representations

A subset F of a group G is called irreducibly faithful if G has an irreducible unitary representation whose kernel does not contain any non-trivial element of F. We say that G has property P(n) if every subset of size at most n is irreducibly faithful. By a classical result o

From playlist Groupes, géométrie et analyse : conférence en l'honneur des 60 ans d'Alain Valette

Introduction to Differential Inequalities

What is a differential inequality and how are they useful? Inequalities are a very practical part of mathematics: They give us an idea of the size of things -- an estimate. They can give us a location for things. It is usually far easier to satisfy assumptions involving inequalities t

From playlist Advanced Studies in Ordinary Differential Equations

Irreducibility (mathematics)

Related pages