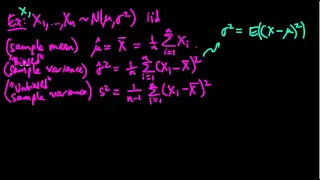
Definition of an estimator. Examples of estimators. Definition of an unbiased estimator.
From playlist Machine Learning

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

The method of determining eigenvalues as part of calculating the sets of solutions to a linear system of ordinary first-order differential equations.
From playlist A Second Course in Differential Equations

#2 Idenitfying Irrational numbers
An example that helps in identifying irrational numbers and understanding the basic concepts of irrational numbers.
From playlist Middle School This Year

From playlist filter (less comfortable)

Draw Perfect Freehand Circles!
Super simple idea that allows you to draw a perfect freehand circle. Use it to win bets, or just impress your friends!
From playlist How to videos!

[ANT04] Counting ideal classes
We don't always get unique factorisation. In those cases, can we measure how badly this uniqueness fails?
From playlist [ANT] An unorthodox introduction to algebraic number theory

Abstract Algebra | Ideals of quotients of PIDs
We prove that every ideal of a quotient of a principal ideal domain is also principal. Notice that the new space may not be an integral domain, so it is sometimes called a principal ring. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http:
From playlist Abstract Algebra

Abstract Algebra | Introduction to Principal Ideal Domains (PIDs)
After introducing the notion of a principal ideal domain (pid), we give some examples, and prove some simple results. Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.michael-penn.net Randolph College Math: http://www.randolphcolle
From playlist Abstract Algebra

Visual Group Theory, Lecture 7.3: Ring homomorphisms
Visual Group Theory, Lecture 7.3: Ring homomorphisms A ring homomorphism is a structure preserving map between rings, which means that f(x+y)=f(x)+f(y) and f(xy)=f(x)f(y) both must hold. The kernel is always a two-sided ideal. There are four isomorphism theorems for rings, which are compl
From playlist Visual Group Theory

RNT2.1. Maximal Ideals and Fields
Ring Theory: We now consider special types of rings. In this part, we define maximal ideals and explore their relation to fields. In addition, we note three ways to construct fields.
From playlist Abstract Algebra

Proof: Ideal of a Ring is Proper iff it has no Units | Abstract Algebra
An ideal of a ring with identity is proper if and only if the ideal contains no units of the ring. We prove this result in today's abstract algebra video lesson! Remember that an ideal, I, of a ring, R, is an additive subgroup of I such that for all r in R and x in I, r*x and x*r are also
From playlist Abstract Algebra

Abstract Algebra | Principal Ideals of a Ring
We define the notion of a principal ideal of a ring and give some examples. We also prove that all ideals of the integers are principal ideals, that is, the integers form a principal ideal domain (PID). http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://
From playlist Abstract Algebra

Lecture 8. PIDs and Euclidean domains
From playlist Abstract Algebra 2

Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields
Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields A left (resp., right) ideal of a ring R is a subring that is invariant under left (resp., right) multiplication. Two-sided ideals are those that are both left and right ideals. This is the analogue of normal subgr
From playlist Visual Group Theory

Rings 6 Prime and maximal ideals
This lecture is part of an online course on rings and modules. We discuss prime and maximal ideals of a (commutative) ring, use them to construct the spectrum of a ring, and give a few examples. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj5
From playlist Rings and modules

An introduction to modelling with higher order differential equations.
From playlist Differential Equations


