
Divisibility, Prime Numbers, and Prime Factorization
Now that we understand division, we can talk about divisibility. A number is divisible by another if their quotient is a whole number. The smaller number is a factor of the larger one, but are there numbers with no factors at all? There's some pretty surprising stuff in this one! Watch th
From playlist Mathematics (All Of It)

Jeff Calder: "An intro to concentration of measure with applications to graph-based l... (Part 2/2)"
Watch part 1/2 here: https://youtu.be/Q5fB5Ldzo-g High Dimensional Hamilton-Jacobi PDEs Tutorials 2020 "An introduction to concentration of measure with applications to graph-based learning (Part 2/2)" Jeff Calder, University of Minnesota - Twin Cities Abstract: We will give a gentle in
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

Bernoulli Differential Equation x*dy/dx + y = 1/y^2
Bernoulli Differential Equation x*dy/dx + y = 1/y^2 If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Zill DE 2.5 Solutions by Substitutions

General strong polarization - Madhu Sudan
Computer Science/Discrete Mathematics Seminar I Topic: Locally symmetric spaces: pp-adic aspects Speaker: General strong polarization Affiliation: Harvard University Date: December 4, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Solve a Bernoulli Differential Equation Initial Value Problem
This video provides an example of how to solve an Bernoulli Differential Equations Initial Value Problem. The solution is verified graphically. Library: http://mathispower4u.com
From playlist Bernoulli Differential Equations

Lagrange multipliers: 2 constraints
Free ebook http://tinyurl.com/EngMathYT A lecture showing how to apply the method of Lagrange multipliers where two contraints are involved.
From playlist Lagrange multipliers
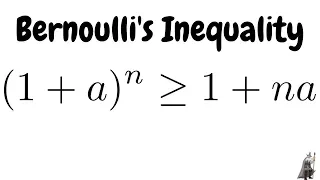
Proof of Bernoulli's Inequality using Mathematical Induction
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Bernoulli's Inequality using Mathematical Induction
From playlist Proofs

B24 Introduction to the Bernoulli Equation
The Bernoulli equation follows from a linear equation in standard form.
From playlist Differential Equations

C73 Introducing the theorem of Frobenius
The theorem of Frobenius allows us to calculate a solution around a regular singular point.
From playlist Differential Equations

24. Martingales: Stopping and Converging
MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

Peter Imkeller: An introduction to BSDE
Abstract: Backward stochastic differential equations have been a very successful and active tool for stochastic finance and insurance for some decades. More generally they serve as a central method in applications of control theory in many areas. We introduce BSDE by looking at a simple ut
From playlist Probability and Statistics

Xu Zhendong - From the Littlewood-Paley-Stein Inequality to the Burkholder-Gundy Inequality
We solve a question asked by Xu about the order of optimal constants in the Littlewood-Paley-Stein inequality. This relies on a construction of a special diffusion semi-group associated with a martingale which relates the Littlewood G-function with the martingale square function pointwise.
From playlist Annual meeting “Arbre de Noël du GDR Géométrie non-commutative”

MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011

20 Tutorial by Ruediger - Stochastic Integration & SDEs
PROGRAM NAME :WINTER SCHOOL ON STOCHASTIC ANALYSIS AND CONTROL OF FLUID FLOW DATES Monday 03 Dec, 2012 - Thursday 20 Dec, 2012 VENUE School of Mathematics, Indian Institute of Science Education and Research, Thiruvananthapuram Stochastic analysis and control of fluid flow problems have
From playlist Winter School on Stochastic Analysis and Control of Fluid Flow

Hans Föllmer: Entropy, energy, and optimal couplings on Wiener space
HYBRID EVENT Recorded during the meeting "Advances in Stochastic Control and Optimal Stopping with Applications in Economics and Finance" the September 12, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video a
From playlist Probability and Statistics

Introduction to additive combinatorics lecture 14.6 --- The U3 norm is a norm
I have been referring to the U3 norm as a norm, but the fact that it is a norm is something that needs to be proved. The proof resembles the proof that the L2 norm is a norm -- that is, first one proves a generalized Cauchy-Schwarz inequality and then from that one deduces the triangle ine
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)


