
What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Mertens Conjecture Disproof and the Riemann Hypothesis | MegaFavNumbers
#MegaFavNumbers The Mertens conjecture is a conjecture is a conjecture about the distribution of the prime numbers. It can be seen as a stronger version of the Riemann hypothesis. It says that the Mertens function is bounded by sqrt(n). The Riemann hypothesis on the other hand only require
From playlist MegaFavNumbers

Ptolemy's theorem and generalizations | Rational Geometry Math Foundations 131 | NJ Wildberger
The other famous classical theorem about cyclic quadrilaterals is due to the great Greek astronomer and mathematician, Claudius Ptolemy. Adopting a rational point of view, we need to rethink this theorem to state it in a purely algebraic way, without resort to `distances' and the correspon
From playlist Math Foundations
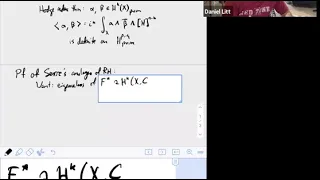
Étale cohomology Lecture II, 8/25/2020
Serre's complex analogue of the Riemann hypothesis, étale morphisms, intro to sites
From playlist Étale cohomology and the Weil conjectures

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics

God's Binomial Identity. #SoME2
My submission for SoME2. Please support my research https://paypal.me/feralmathematician?locale.x=en_US
From playlist Summer of Math Exposition 2 videos

The Collatz Conjecture and Fractals
Visualizing the dynamics of the Collatz Conjecture though fractal self-similarity. Support this channel: https://www.patreon.com/inigoquilez Tutorials on maths and computer graphics: https://iquilezles.org Code for this video: https://www.shadertoy.com/view/llcGDS Donate: http://paypal.m
From playlist Maths Explainers

Weil conjectures 6: etale cohomology of a curve
We give an overview of how to calculate the etale cohomology of a nonsinguar projective curve over an algebraically closed field with coefficients Z/nZ with n invertible. We simply assume a lot of properties of etale cohomology without proving (or even defining) them.
From playlist Algebraic geometry: extra topics

The Halting Problem - An Impossible Problem to Solve
Start learning today with SkillShare: https://skl.sh/upandatom2 Alan Turing proved that the Halting Problem was impossible for Turing machines (computers) to solve. Come find out how. The quantum computer game I talked about: https://phys.cam/game/ This video was co-written by my supe
From playlist Computer Science

Brauer groups, Severi-Brauer schemes, Azumaya algebras, twisted sheaves
From playlist Étale cohomology and the Weil conjectures

Andrew Wiles | Twenty Years of Number Theory | 1998
Notes for this talk: https://drive.google.com/file/d/1eJXPwL772Z00egvLjO3VHmvCv7mwcv6Q/view?usp=sharing Twenty Years of Number Theory Andrew Wiles Princeton University ICM Berlin 19.08.1998 https://www.mathunion.org/icm/icm-videos/icm-1998-videos-berlin-germany/icm-berlin-videos-2708
From playlist Number Theory

3 AMAZING Carbon Snake Experiments - Chemistry Demos
Thanks to MEL Science for sponsoring this video. Get your MEL Science kit subscription here: https://melscience.com/s2z/ Enter this code to save 50%: Craig50 The Carbon Snake is a classic chemistry demonstration for showing decomposition and combustion reactions in the chemistry lab. Cra
From playlist Science Experiments!

Bowling Ball Cannon in a Jeep!
Craig Beals and the crew at Beals Science build a massive bowling ball cannon in an old Postal Delivery Jeep. Watch as the cannon launches bowling balls more than two miles and see what happens when a bowling ball fired from the cannon meets a toilet! SUBSCRIBE by clicking here: https://g
From playlist Science Experiments!
On descending cohomology geometrically - Sebastian Casalaina-Martin
Sebastian Casalaina-Martin University of Colorado at Boulder January 20, 2015 In this talk I will present some joint work with Jeff Achter concerning the problem of determining when the cohomology of a smooth projective variety over the rational numbers can be modeled by an abelian variet
From playlist Mathematics

Science Spot with Craig Beals on Montana This Morning
Science Spot with Craig Beals on Montana This Morning
From playlist Science Spot on CBS - KTVQ with Craig Beals

Disappearing Water Trick - Science or Magic?
Craig Beals explains the science behind a magic trick he uses in his classroom to introduce polymers. Water is added to Sodium polyacrylate in this experiment and the polymer soaks it up. Craig also answers the question: how do diapers work? He explains how sodium polyacrylate is used in d
From playlist Science Experiments!

ABC Intro - part 1 - What is the ABC conjecture?
This videos gives the basic statement of the ABC conjecture. It also gives some of the consequences.
From playlist ABC Conjecture Introduction

Invisible Labs with Craig Beals Season 2 Trailer
Invisible Labs with Craig Beals is back! Season 2 of FLIR's educational series takes things to a whole new level - hosted by Craig Beals, 2015 Montana Teacher of the Year, we will be tackling scientific subjects all while visualizing the energy of the invisible world around use with therma
From playlist Invisible Labs with Craig Beals - FLIR

Weil conjectures 4 Fermat hypersurfaces
This talk is part of a series on the Weil conjectures. We give a summary of Weil's paper where he introduced the Weil conjectures by calculating the zeta function of a Fermat hypersurface. We give an overview of how Weil expressed the number of points of a variety in terms of Gauss sums. T
From playlist Algebraic geometry: extra topics

Gallium - How to Make a Disappearing Spoon
Craig Beals shows how to make a gallium spoon to do the disappearing spoon trick. Gallium melts at 85 degrees F so a spoon made of gallium will melt in warm water. This trick was performed in the 1800's by chemists at tea parties in Europe and the trick lives on today at Beals Science. Bu
From playlist Science Experiments!