
Introduction to Vector Fields This video discusses, 1) The definition of a vector field. 2) Examples of vector fields including the gradient, and various velocity fields. 3) The definition of a conservative vector field. 4) The definition of a potential function. 5) Test for conservative
From playlist Calculus 3

Lie derivatives of differential forms
Introduces the lie derivative, and its action on differential forms. This is applied to symplectic geometry, with proof that the lie derivative of the symplectic form along a Hamiltonian vector field is zero. This is really an application of the wonderfully named "Cartan's magic formula"
From playlist Symplectic geometry and mechanics

Worldwide Calculus: Vector Fields
Lecture on 'Vector Fields' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Integration and Vector Fields

Multivariable Calculus | What is a vector field.
We introduce the notion of a vector field and give some graphical examples. We also define a conservative vector field with examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Multivariable Calculus

This video explains the definition of a vector space and provides examples of vector spaces.
From playlist Vector Spaces

11_7_1 Potential Function of a Vector Field Part 1
The gradient of a function is a vector. n-Dimensional space can be filled up with countless vectors as values as inserted into a gradient function. This is then referred to as a vector field. Some vector fields have potential functions. In this video we start to look at how to calculat
From playlist Advanced Calculus / Multivariable Calculus

Free ebook http://tinyurl.com/EngMathYT Basic example of how to sketch a constant vector field.
From playlist Engineering Mathematics

Free ebook http://tinyurl.com/EngMathYT A basic introduction to vector fields discussing the need for vector fields and some of the basic mathematics associated with them.
From playlist Engineering Mathematics

Brent Pym: Holomorphic Poisson structures - lecture 2
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Symplectic Dynamics of Integrable Hamiltonian Systems - Alvaro Pelayo
Alvaro Pelayo Member, School of Mathematics April 4, 2011 I will start with a review the basic notions of Hamiltonian/symplectic vector field and of Hamiltonian/symplectic group action, and the classical structure theorems of Kostant, Atiyah, Guillemin-Sternberg and Delzant on Hamiltonian
From playlist Mathematics

Equivariant structures in mirror symmetry - James Pascaleff
James Pascaleff University of Illinois at Urbana-Champaign October 17, 2014 When a variety XX is equipped with the action of an algebraic group GG, it is natural to study the GG-equivariant vector bundles or coherent sheaves on XX. When XX furthermore has a mirror partner YY, one can ask
From playlist Mathematics

Erlend Fornæss Wold: Symplectic Carleman approximation on co-adjoint orbits
For a complex Lie group $G$ with a real form $G_{0}\subset G$, we prove that any Hamiltionian automorphism $\phi$ of a coadjoint orbit $\mathcal{O}_{0}$ of $G_{0}$ whose connected components are simply connected, may be approximated by holomorphic $O_{0}$-invariant symplectic automorphism
From playlist Analysis and its Applications

Brent Pym: Holomorphic Poisson structures - lecture 3
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Alberto Cattaneo: An introduction to the BV-BFV Formalism
Abstract: The BV-BFV formalism unifies the BV formalism (which deals with the problem of fixing the gauge of field theories on closed manifolds) with the BFV formalism (which yields a cohomological resolution of the reduced phase space of a classical field theory). I will explain how this
From playlist Topology
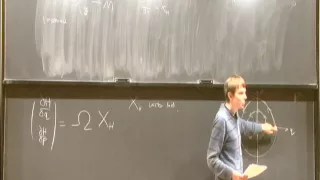
How to Find Periodic Orbits and Exotic Symplectic Manifolds - Mark McLean
Mark McLean Massachusetts Institute of Technology; Member, School of Mathematics October 15, 2012 I will give an introduction to symplectic geometry and Hamiltonian systems and then introduce an invariant called symplectic cohomology. This has many applications in symplectic geometry and
From playlist Mathematics

David Mond: The intersection form, logarithmic vector fields, and the Severi strata..
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Pavel Etingof - "D-modules on Poisson varieties and Poisson traces"
Pavel Etingof delivers a research talk on "D-modules on Poisson varieties and Poisson traces" at the Worldwide Center of Mathematics
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Act globally, compute...points and localization - Tara Holm
Tara Holm Cornell University; von Neumann Fellow, School of Mathematics October 20, 2014 Localization is a topological technique that allows us to make global equivariant computations in terms of local data at the fixed points. For example, we may compute a global integral by summing inte
From playlist Mathematics
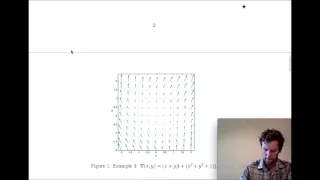
MATH2018 Lecture 3.2 Vector Fields
We discuss the concept of a vector field and introduce some basic tools for understanding them: divergence and curl.
From playlist MATH2018 Engineering Mathematics 2D
