
Integrate cosine using u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

What is the constant rule of integration
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Learn how to use u substitution to integrate a polynomial
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Apply u substitution to a polynomial
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Differential Equations | Convolution: Definition and Examples
We give a definition as well as a few examples of the convolution of two functions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Differential Equations

Jean Écalle - Resurgence’s two Main Types and Their Signature Complications...
Resurgence’s two Main Types and Their Signature Complications: Tessellation, Isography, Autarchy Quite specific challenges attend the move from equational resurgence (i.e. resurgence in a singular variable –the main type in frequency and importance) to coequational re
From playlist Resurgence in Mathematics and Physics

How to integrate when there is a radical in the denominator
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Jacek Dziubański: Selected results in real harmonic analysis in the rational Dunkl setting
HYBRID EVENT Recorded during the meeting "Modern Analysis Related to Root Systems with Applications" the October 19, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathe
From playlist Virtual Conference

Universality of Resurgence in Quantization Theories - 13 June 2018
http://crm.sns.it/event/433 Universality of Resurgence in Quantization Theories Recent mathematical progress in the modern theory of resurgent asymptotic analysis (using trans-series and alien calculus) has recently begun to be applied systematically to many current problems of interest,
From playlist Centro di Ricerca Matematica Ennio De Giorgi
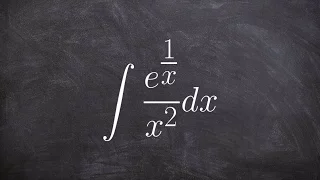
How to integrate exponential expression with u substitution
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Coulomb Branches of 3d N=4 SUSY Gauge Theories and Bow Varieties I
Hiraku Nakajima Kavli IPMU, Japan
From playlist Distinguished Visitors Lecture Series

Transcendental Functions 17 The Indefinite Integral of 1 over u du Example 1.mov
Example problems involving the integral of u to the power negative 1 du.
From playlist Transcendental Functions

Felix Otto: Singular SPDE with rough coefficients
Abstract: We are interested in parabolic differential equations (∂t−a∂2x)u=f with a very irregular forcing f and only mildly regular coefficients a. This is motivated by stochastic differential equations, where f is random, and quasilinear equations, where a is a (nonlinear) function of u.
From playlist Probability and Statistics

Pascal Auscher: 30 years of T(b) theorems
Abstract: The T(b) theorem proved 30 years ago by David, Journé and Semmes, following a first result of McIntosh and Meyer, has proved to be a powerful and versatile tool for a number of applications. We will discuss history and main applications including recent ones. Recording during th
From playlist Analysis and its Applications

Modulation Spaces and Applications to Hartree-Fock Equations by Divyang Bhimani
We discuss some ongoing interest (since last decade) in use of modulation spaces in harmonic analysis and its connection to nonlinear dispersive equations. In particular, we shall discuss results on Hermite multiplier and composition operators on modulation spaces. As an application to the
From playlist ICTS Colloquia

Lec 35 | MIT 18.085 Computational Science and Engineering I, Fall 2008
Lecture 35: Convolution equations: deconvolution; convolution in 2D License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.085 Computational Science & Engineering I, Fall 2008

Colloquium MathAlp 2018 - Stéphane Jaffard
Quelle est la régularité de la fonction de Brjuno ? Introduite par J.-C. Yoccoz, la fonction de Brjuno fournit une information importante sur les problèmes de petits diviseurs analytiques. Elle semble ne posséder aucune régularite en un sens raisonnable: elle n'est nulle part localement
From playlist Colloquiums MathAlp

Dirichlet Eta Function - Integral Representation
Today, we use an integral to derive one of the integral representations for the Dirichlet eta function. This representation is very similar to the Riemann zeta function, which explains why their respective infinite series definition is quite similar (with the eta function being an alte rna
From playlist Integrals

Learn how to integrate a rational expression by simplifying first with rational powers
👉 Learn how to evaluate the integral of a function. The integral, also called antiderivative, of a function, is the reverse process of differentiation. Integral of a function can be evaluated as an indefinite integral or as a definite integral. A definite integral is an integral in which t
From playlist The Integral

Erik van Erp: Lie groupoids in index theory 2
The lecture was held within the framework of the Hausdorff Trimester Program Non-commutative Geometry and its Applications. 9.9.2014
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"