
What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics
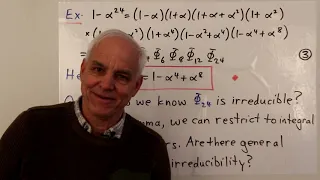
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Applications of additive combinatorics to Diophantine equations - Alexei Skorobogatov
Alexei Skorobogatov Imperial College London April 10, 2014 The work of Green, Tao and Ziegler can be used to prove existence and approximation properties for rational solutions of the Diophantine equations that describe representations of a product of norm forms by a product of linear poly
From playlist Mathematics

Physicist Explains Wikipedia Page: The Schrodinger Equation
Why are Wikipedia Physics pages so difficult to understand? Hey guys, I'm back with a new video! This time, I'm looking at how certain Wikipedia pages can be so complicated to understand, and so here's a Wikipedia page made easy! Now I can totally understand that a wiki page is meant to p
From playlist Quantum Physics by Parth G

Strong approximation for a family of norm varieties - Xu - Workshop 1 - CEB T2 2019
Fei Xu (Capital Normal University) / 23.05.2019 Strong approximation for a family of norm varietiesLet L/k be a finite extension of number fields and q(t) be a polynomial over k. It is a classical problem to study weak approximation for the family of norm varieties defined by NL/k(x) = q
From playlist 2019 - T2 - Reinventing rational points

A quantum particle starting in a well of a periodic egg carton potential
Like the video https://youtu.be/DzIZwCeaVkM this one shows a simulation of a quantum particle in a periodic potential. The point of view rotates around the potential landscape, which remains fixed in space. While on the previous video, the initial state was a Gaussian wave packet located n
From playlist Schrödinger's equation

How the Schrodinger Equation Predicts Real Life (and Why It's So Difficult) - Quantum Mech Parth G
Understanding the Schrodinger Equation theoretically is very useful... but the main aim of the equation is to predict what happens in real life! In this video, we'll be looking at how the Schrodinger Equation can be used to predict the behaviour of a hydrogen atom. To do this, we'll first
From playlist Quantum Physics by Parth G

Squares represented by a product of three ternary (...) - Harpaz - Workshop 2 - CEB T2 2019
Yonatan Harpaz (Université Paris Nord) / 27.06.2019 Squares represented by a product of three ternary quadratic forms, and a homogeneous variant of a method of Swinnerton-Dyer. Let k be a number field. In this talk we will consider K3 surfaces over k which admit a degree 2 map to the pr
From playlist 2019 - T2 - Reinventing rational points

Separation of variables and the Schrodinger equation
A brief explanation of separation of variables, application to the time-dependent Schrodinger equation, and the solution to the time part. (This lecture is part of a series for a course based on Griffiths' Introduction to Quantum Mechanics. The Full playlist is at http://www.youtube.com/
From playlist Mathematical Physics II - Youtube

Quantum Mechanics 5a - Schrödinger Equation I
Building on Louis de Broglie's hypothesis of "electron waves," Erwin Schrödinger develops a wave equation for electrons. The playlist: http://www.youtube.com/playlist?list=PL193BC0532FE7B02C
From playlist Quantum Mechanics

Andrzej Schinzel: The Congruence f ( x ) + g ( y ) + c = 0 (mod xy )
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

Small Height and Infinite Non-Abelian Extensions - Philipp Habegger
Philipp Habegger University of Frankfurt; Member, School of Mathematics April 8, 2013 he Weil height measures the “complexity” of an algebraic number. It vanishes precisely at 0 and at the roots of unity. Moreover, a finite field extension of the rationals contains no elements of arbitrari
From playlist Mathematics

29C3: Time is NOT on your Side (EN)
Speaker: Sebastian Schinzel Mitigating Timing Side Channels on the Web In this year's talk, I tie on my 28c3 talk and present timing side channels from a defending viewpoint: How can one mitigate timing side channels? Aren't random delays sufficient to prevent timing side channels in pra
From playlist 29C3: Not my department

29C3: Was ist, was kann, was soll Gender Studies Informatik? (DE)
Speaker: Britta Schinzel Weltbilder der Informatik sind in mancher Hinsicht denen in der Hacker- und Hackerinnen-Community nicht unähnlich. Was ist? Allgemein werden die Gender-Forschungen zur Technik unterteilt in die Kategorien: 1. Frauen, Männer, Altersgruppen, Ethnien, soziale Schic
From playlist 29C3: Not my department

For more information visit: http://bit.ly/28C3_information To download the video visit: http://bit.ly/28C3_videos Playlist 28C3: http://bit.ly/28C3_playlist Speaker: Sebastian Schinzel Exploiting Timing Side Channel Vulnerabilities on the Web Timing side channel attacks are non-
From playlist 28C3: Behind Enemy Lines

The Schrodinger equation made simple | Linearity
We've talked about the quantum state plenty- but what happens to it over time? That's exactly the question the Schrodinger equation solves. This video we talk about 'Linearity'. In the next video we discuss the equation itself and its derivation. Click here fore that: https://youtu.be/DEgW
From playlist Quantum Mechanics (all the videos)

Dealing with Schrodinger's Equation - The Hamiltonian
https://www.patreon.com/edmundsj If you want to see more of these videos, or would like to say thanks for this one, the best way you can do that is by becoming a patron - see the link above :). And a huge thank you to all my existing patrons - you make these videos possible. Schrodinger's
From playlist Quantum Mechanics

Reducible fibers and monodromy of polynomial maps - Danny Neftin
Joint IAS/Princeton University Number Theory Seminar Topic: Reducible fibers and monodromy of polynomial maps Speaker: Danny Neftin Date: October 28, 2021 For a polynomial f∈ℚ[x], Hilbert's irreducibility theorem asserts that the fiber f−1(a) is irreducible over ℚ for all values a∈ℚ out
From playlist Mathematics

Jan-Hendrik Evertse: On Scmidt's subspace theorem
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

Lecture 9 | Machine Learning (Stanford)
Lecture by Professor Andrew Ng for Machine Learning (CS 229) in the Stanford Computer Science department. Professor Ng delves into learning theory, covering bias, variance, empirical risk minimization, union bound and Hoeffding's inequalities. This course provides a broad introduction
From playlist Lecture Collection | Machine Learning