
How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation

Riemann Sum Defined w/ 2 Limit of Sums Examples Calculus 1
I show how the Definition of Area of a Plane is a special case of the Riemann Sum. When finding the area of a plane bound by a function and an axis on a closed interval, the width of the partitions (probably rectangles) does not have to be equal. I work through two examples that are rela
From playlist Calculus

Understanding and computing the Riemann zeta function
In this video I explain Riemann's zeta function and the Riemann hypothesis. I also implement and algorithm to compute the return values - here's the Python script:https://gist.github.com/Nikolaj-K/996dba1ff1045d767b10d4d07b1b032f
From playlist Programming

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Midpoint riemann sum approximation
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist The Integral

We present a proof of the Hopf-Rinow theorem. For more details see do Carmo's "Riemannian geometry" Chapter 7.
From playlist Differential geometry

Learn how to find the position function given the velocity and acceleration, parti
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation
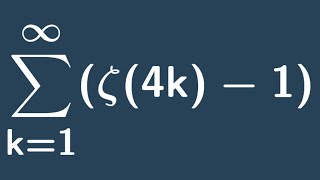
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

C. Leininger - Teichmüller spaces and pseudo-Anosov homeomorphism (Part 2)
I will start by describing the Teichmuller space of a surface of finite type from the perspective of both hyperbolic and complex structures and the action of the mapping class group on it. Then I will describe Thurston's compactification of Teichmuller space, and state his classification t
From playlist Ecole d'été 2018 - Teichmüller dynamics, mapping class groups and applications

John H. Hubbard: Introduction to Thurston’s theorems
HYBRID EVENT Recorded during the meeting "Advancing Bridges in Complex Dynamics" the September 20, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM'
From playlist Topology

Finiteness theorems for the space of holomorphic mappings by Jaikrishnan Janardhanan
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Quadratic differentials and measured foliations on Riemann surfaces by Subhojoy Gupta
Program : Integrable? ?systems? ?in? ?Mathematics,? ?Condensed? ?Matter? ?and? ?Statistical? ?Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

Jacob Lurie: A Riemann-Hilbert Correspondence in p-adic Geometry Part 2
At the start of the 20th century, David Hilbert asked which representations can arise by studying the monodromy of Fuchsian equations. This question was the starting point for a beautiful circle of ideas relating the topology of a complex algebraic variety X to the study of algebraic diffe
From playlist Felix Klein Lectures 2022

This is the second part of a proof of the Riemann Roch theorem. In it we prove Roch's part of the theorem ("Serre duality") which states that i(D) = l(K-D). We first work over the complex numbers where we can use the residue calculus. This gives two key points: a 1-form has a well defined
From playlist Algebraic geometry: extra topics

The 3 Best Books on Complex Analysis
I describe my three favorite books for an introduction to complex analysis, and conclude with some remarks about a few other books. Hope this is helpful for both students and instructors! 0:00 Book 1: Greene and Krantz 6:08 Book 2: Stein and Shakarchi 10:14 Book 3: Ablowitz and Fokas 13:4
From playlist Math

8ECM Plenary Lecture: Franc Forstnerič
From playlist 8ECM Plenary Lectures

Introduction to quadrature domains (Lecture 3) by Kaushal Verma
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Projective structures on Riemann surfaces and their monodromy by Subhojoy Gupta
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

This talk is the first of two talks that give a proof of the Riemann Roch theorem, in the spacial case of nonsingular complex plane curves. We divide the Riemann-Roch theorem into 3 pieces: Riemann's theorem, a topological theorem identifying the three definitions of the genus, and Roch'
From playlist Algebraic geometry: extra topics