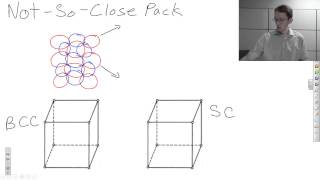
Not-So-Close Packed Crystal Structures
A description of two crystal structures that are created from not-so-close packed structures.
From playlist Atomic Structures and Bonding

What is the definition of a regular polygon and how do you find the interior angles
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between a regular and irregular polygon
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What is the difference between a regular and irregular polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are the names of different types of polygons based on the number of sides
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

What are four types of polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons

👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons
Jon Pakianathan (5/7/19): On a canonical construction of tessellated surfaces from finite groups
Title: On a canonical construction of tessellated surfaces from finite groups Abstract: In this talk we will discuss an elementary construction that associates to the non-commutative part of a finite group’s multiplication table, a finite collection of closed, connected, oriented surfaces
From playlist AATRN 2019

Monadic Parsers at the Input Boundary
When reading a byte stream over the process I/O boundary, the first thing which everyone should do is to parse the byte stream with a monadic parser. The talk will discuss Processes and input byte streams. Monadic parsers. What they are and why they matter. The design and use of the pure
From playlist Functional Programming

Brent Pym: Holomorphic Poisson structures - lecture 3
The notion of a Poisson manifold originated in mathematical physics, where it is used to describe the equations of motion of classical mechanical systems, but it is nowadays connected with many different parts of mathematics. A key feature of any Poisson manifold is that it carries a cano
From playlist Virtual Conference

Martin Hairer Mini-course 2: Introduction to Regularity Structures
SMRI-MATRIX Symposium with Martin Hairer 18 February 2021: Mini-course 2 Title: Introduction to Regularity Structures Part 2 Symposium website: https://sites.google.com/monash.edu/symposium-with-martin-hairer/home Question from audience member (1:01:26): Is it possible to encode non-l
From playlist Symposium with Martin Hairer

Konstantin Matetski (Columbia) -- Directed mean curvature flow in noisy environment
We consider the directed mean curvature flow evolving on the plane in a weak disordered Gaussian environment. A simpler version of the model is the quenched KPZ equation with a weak noise. We prove that, when started from a sufficiently regular initial state, a rescaled and renormalized cu
From playlist Columbia Probability Seminar

Konstantin Matetski (Columbia) -- Directed mean curvature flow in noisy environment
We consider the directed mean curvature flow evolving on the plane in a weak disordered Gaussian environment. A simpler version of the model is the quenched KPZ equation with a weak noise. We prove that, when started from a sufficiently regular initial state, a rescaled and renormalized cu
From playlist Columbia Probability Seminar

A stable arithmetic regularity lemma in finite (...) - C. Terry - Workshop 1 - CEB T1 2018
Caroline Terry (Maryland) / 01.02.2018 A stable arithmetic regularity lemma in finite-dimensional vector spaces over fields of prime order In this talk we present a stable version of the arithmetic regularity lemma for vector spaces over fields of prime order. The arithmetic regularity l
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Josef Teichmann: An elementary proof of the reconstruction theorem
CIRM VIRTUAL EVENT Recorded during the meeting "Pathwise Stochastic Analysis and Applications" the March 09, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematician
From playlist Virtual Conference

Chris WENDL - 2/3 Classical transversality methods in SFT
In this talk I will discuss two transversality results that are standard but perhaps not so widely understood: (1) Dragnev's theorem that somewhere injective curves in symplectizations are regular for generic translation-invariant J, and (2) my theorem on automatic transversality in 4-dime
From playlist 2015 Summer School on Moduli Problems in Symplectic Geometry

Ana Balibanu: The partial compactification of the universal centralizer
Abstract: Let G be a semisimple algebraic group of adjoint type. The universal centralizer is the family of centralizers in G of regular elements in Lie(G), parametrized by their conjugacy classes. It has a natural symplectic structure, obtained by Hamiltonian reduction from the cotangent
From playlist Algebra

Classifying a polygon in two different ways ex 4
👉 Learn about polygons and how to classify them. A polygon is a plane shape bounded by a finite chain of straight lines. A polygon can be concave or convex and it can also be regular or irregular. A concave polygon is a polygon in which at least one of its interior angles is greater than 1
From playlist Classify Polygons