
Euler-Mascheroni XIV: A Curious Rational Zeta Series
Channel social media: Instagram: @whatthehectogon https://www.instagram.com/whatthehect... Twitter: @whatthehectogon https://twitter.com/whatthehectogon Any questions? Leave a comment below or email me at the misspelled whatthehectagon@gmail.com Today we're combining the last two E-M
From playlist Analysis

Some identities involving the Riemann-Zeta function.
After introducing the Riemann-Zeta function we derive a generating function for its values at positive even integers. This generating function is used to prove two sum identities. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function
More identities involving the Riemann-Zeta function!
By applying some combinatorial tricks to an identity from https://youtu.be/2W2Ghi9idxM we are able to derive two identities involving the Riemann-Zeta function. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist The Riemann Zeta Function

Fourier Series Coefficients (where did they come from?)
Learn how to derive the Fourier series coefficients formulas. Remember, a Fourier series is a series representation of a function with sin(nx) and cos(nx) as its building blocks. Meanwhile, a Taylor series is a series representation of a function with x^n as its building blocks. These are
From playlist Fourier Series

This video introduces the harmonic series, explains why it is divergent and also examples infinite series that resemble the harmonic series. Site: http://mathispower4u.com
From playlist Infinite Series

Number Theory 1.1 : Product Formula for the Zeta Function
In this video, I prove Euler's product formula for the Riemann Zeta function. Email : fematikaqna@gmail.com Code : https://github.com/Fematika/Animations Notes : None yet
From playlist Number Theory
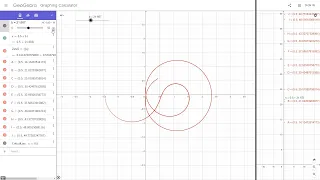
The Riemann Hypothesis - Picturing The Zeta Function
in this chapter i will show how to visualize the zeta and eta functions in the proper way meaning that everything on those two functions is made out of spirals all over the grid and the emphasis in this chapter will be on the center points of the spirals mainly the divergent spirals 0:00
From playlist Summer of Math Exposition Youtube Videos

Analytic Continuation and the Zeta Function
Where do complex functions come from? In this video we explore the idea of analytic continuation, a powerful technique which allows us to extend functions such as sin(x) from the real numbers into the complex plane. Using analytic continuation we can finally define the zeta function for co
From playlist Analytic Number Theory

Michael Hoffman: Multiple zeta values and alternating MZVs arising from a combinatorial problem
The lecture was held within the framework of the Hausdorff Trimester Program: Periods in Number Theory, Algebraic Geometry and Physics. Abstract: Guy Louchard posed the problem of obtaining the general term of an asymptotic expansion of a certain definite integral. This led several peop
From playlist Workshop: "Periods and Regulators"

Wim Veys : Zeta functions and monodromy
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

Henri Darmon: Andrew Wiles' marvelous proof
Abstract: Pierre de Fermat famously claimed to have discovered “a truly marvelous proof” of his last theorem, which the margin in his copy of Diophantus' Arithmetica was too narrow to contain. Fermat's proof (if it ever existed!) is probably lost to posterity forever, while Andrew Wiles' p
From playlist Abel Lectures

Birch Swinnerton-Dyer conjecture: Introduction
This talk is an graduate-level introduction to the Birch Swinnerton-Dyer conjecture in number theory, relating the rank of the Mordell group of a rational elliptic curve to the order of the zero of its L series at s=1. We explain the meaning of these terms, describe the motivation for the
From playlist Math talks

Introduction to Modular Forms - Part 7 of 8
“Introduction to Modular Forms,” by Keith Conrad. Topics include Eisenstein series and q-expansions, applications to sums of squares and zeta-values, Hecke operators, eigenforms, and the L-function of a modular form. This is a video from CTNT, the Connecticut Summer School in Number Theor
From playlist CTNT 2016 - "Introduction to Modular Forms" by Keith Conrad

Weil conjectures 2: Functional equation
This is the second lecture about the Weil conjectures. We show that the Riemann-Roch theorem implies the rationality and functional equation of the zeta function of a curve over a finite field.
From playlist Algebraic geometry: extra topics

Yuri Tschinkel, Height zeta functions
VaNTAGe seminar May 11, 2021 License: CC-BY-NC-SA
From playlist Manin conjectures and rational points
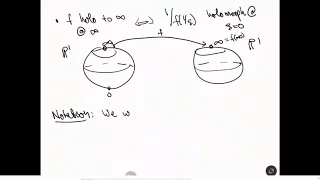
MATH 331: Compactifying CC - part 4 - Endomorphisms of PP^1 are Rational
In this video we finally prove that holomorphic maps from PP^1 to itself are rational.
From playlist The Riemann Sphere

CTNT 2018 - "L-functions and the Riemann Hypothesis" (Lecture 3) by Keith Conrad
This is lecture 3 of a mini-course on "L-functions and the Riemann Hypothesis", taught by Keith Conrad, during CTNT 2018, the Connecticut Summer School in Number Theory. For more information about CTNT and other resources and notes, see https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2018 - "L-functions and the Riemann Hypothesis" by Keith Conrad

Values of L-Functions and Modular Forms - Chris Skinner
Chris Skinner Princeton University; Member, School of Mathematics October 25, 2010 This will be an introduction to special value formulas for L-functions and especially the uses of modular forms in establishing some of them -- beginning with the values of the Riemann zeta function at nega
From playlist Mathematics

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics
