
C73 Introducing the theorem of Frobenius
The theorem of Frobenius allows us to calculate a solution around a regular singular point.
From playlist Differential Equations

The Frobenius Problem - Method for Finding the Frobenius Number of Two Numbers
Goes over how to find the Frobenius Number of two Numbers.
From playlist ℕumber Theory

Differential Equations | Frobenius' Method part 2
From Garden of the Gods in Colorado Springs, we present a Theorem regarding Frobenius Series solutions to a certain family of second order homogeneous differential equations. An example is also explored. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Series Solutions for Differential Equations
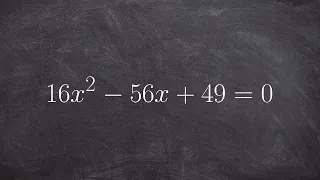
How to find the discriminant and label the solutions of a quadratic
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

How to find the discriminant of a quadratic and label the solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

What is the discriminant and what does it mean
👉 Learn all about the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. The disc
From playlist Discriminant of a Quadratic Equation | Learn About
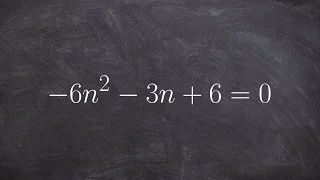
How to use the discriminat to describe your solutions
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

Stanford EE104: Introduction to Machine Learning | 2020 | Lecture 6 - empirical risk minimization
Professor Sanjay Lall Electrical Engineering To follow along with the course schedule and syllabus, visit: http://ee104.stanford.edu To view all online courses and programs offered by Stanford, visit: https://online.stanford.edu/ 0:00 Introduction 0:26 Parametrized predictors 3:09 Tra
From playlist Stanford EE104: Introduction to Machine Learning Full Course
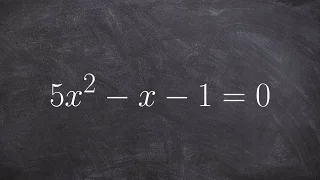
Determine and describe the discriminant
👉 Learn how to determine the discriminant of quadratic equations. A quadratic equation is an equation whose highest power on its variable(s) is 2. The discriminant of a quadratic equation is a formula which is used to determine the type of roots (solutions) the quadratic equation have. T
From playlist Discriminant of a Quadratic Equation

Arithmetic hyperbolic 3-manifolds, perfectoid spaces, and Galois representations II - Peter Scholze
Peter Scholze University of Bonn February 12, 2014 One of the most studied objects in mathematics is the modular curve, which is the quotient of hyperbolic 2-space by the action of SL2z. It is naturally the home of modular forms, but it also admits an algebraic structure. The interplay of
From playlist Mathematics

Differential Equations | Frobenius' Method -- Example 1
From the desert, we present an example of a Frobenius series solution to a second order homogeneous differential equation. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Series Solutions for Differential Equations

Arithmetic hyperbolic 3-manifolds, perfectoid spaces, and Galois representations II - Peter Scholze
Peter Scholze University of Bonn February 12, 2014 One of the most studied objects in mathematics is the modular curve, which is the quotient of hyperbolic 2-space by the action of SL2Z. It is naturally the home of modular forms, but it also admits an algebraic structure. The interplay of
From playlist Mathematics

Kim Manuel Klein: On the Fine-Grained Complexity of the Unbounded SubsetSum and Frobenius Problem
Consider positive integral solutions x e Z^(n+1) to the equation a0 * x0 + ... + an * xn = t. In the so called unbounded subset sum problem, the objective is to decide whether such a solution exists, whereas in the Frobenius problem, the objective is to compute the largest t such that ther
From playlist Workshop: Parametrized complexity and discrete optimization

Jacob Lurie - Tamagawa Numbers and Nonabelian Poincare Duality, I [2013]
Jacob Lurie Wednesday, August 28 3:10PM Tamagawa Numbers and Nonabelian Poincare Duality, I Gelfand Centennial Conference: A View of 21st Century Mathematics MIT, Room 34-101, August 28 - September 2, 2013 Abstract: Let q and q0 be positive definite integral quadratic forms. We say that
From playlist Number Theory

CTNT 2018 - "Elliptic curves over finite fields" (Lecture 3) by Erik Wallace
This is lecture 3 of a mini-course on "Elliptic curves over finite fields", taught by Erik Wallace, during CTNT 2018, the Connecticut Summer School in Number Theory. For more information about CTNT and other resources and notes, see https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2018 - "Elliptic Curves over Finite Fields" by Erik Wallace

Kiran Kedlaya, The Sato-Tate conjecture and its generalizations
VaNTAGe seminar on March 24, 2020 License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Amicable Pairs and Aliquot Cycles for Elliptic Curves
An amicable pair for an elliptic curve E/Q is a pair of primes (p,q) of good reduction for E satisfying #E(Fp) = q and #E(Fq) = p. Aliquot cycles are analogously defined longer cycles. Although rare for non-CM curves, amicable pairs are -- surprisingly -- relatively abundant in the CM case
From playlist My Math Talks

Andrew Sutherland, Arithmetic L-functions and their Sato-Tate distributions
VaNTAGe seminar on April 28, 2020. License: CC-BY-NC-SA Closed captions provided by Jun Bo Lau.
From playlist The Sato-Tate conjecture for abelian varieties

Richard Taylor "Reciprocity Laws" [2012]
Slides for this talk: https://drive.google.com/file/d/1cIDu5G8CTaEctU5qAKTYlEOIHztL1uzB/view?usp=sharing Richard Taylor "Reciprocity Laws" Abstract: Reciprocity laws provide a rule to count the number of solutions to a fixed polynomial equation, or system of polynomial equations, modu
From playlist Number Theory

Differential Equations | Frobenius' Method part 1
From the bridge of the Starship Enterprise, we present a Theorem which will form the basis for a Frobenius solution to a certain family of 2nd order differential equations. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Series Solutions for Differential Equations