
Raimar WULKENHAAR - Solvable Dyson-Schwinger Equations
Dyson-Schwinger equations provide one of the most powerful non-perturbative approaches to quantum field theories. The quartic analogue of the Kontsevich model is a toy model for QFT in which the tower of Dyson-Schwinger equations splits into one non-linear equation for the planar two-point
From playlist Talks of Mathematics Münster's reseachers
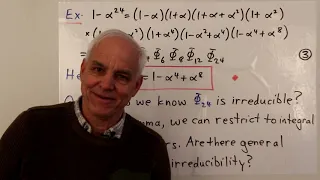
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (4 of 92) The Schrodinger Eqn. "Derived"
Visit http://ilectureonline.com for more math and science lectures! In this video I will “derive” the Schrodinger equation using y(x,y)=Acos(kx-wt). Next video in this series can be seen at: https://youtu.be/GyKk2-0JZ48
From playlist PHYSICS 66.1 QUANTUM MECHANICS - SCHRODINGER EQUATION

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
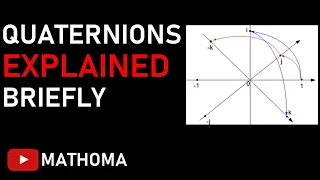
This is a video I have been wanting to make for some time, in which I discuss what the quaternions are, as mathematical objects, and how we do calculations with them. In particular, we will see how the fundamental equation of the quaternions i^2=j^2=k^2=ijk=-1 easily generates the rule for
From playlist Quaternions

How to find the position function given the acceleration function
👉 Learn how to approximate the integral of a function using the Reimann sum approximation. Reimann sum is an approximation of the area under a curve or between two curves by dividing it into multiple simple shapes like rectangles and trapezoids. In using the Reimann sum to approximate the
From playlist Riemann Sum Approximation

Secret of row 10: a new visual key to ancient Pascalian puzzles
NEW (Christmas 2019). Two ways to support Mathologer Mathologer Patreon: https://www.patreon.com/mathologer Mathologer PayPal: paypal.me/mathologer (see the Patreon page for details) Today's video is about a recent chance discovery (2002) that provides a new beautiful visual key to some
From playlist Recent videos

Ch4 Pr4: Taylor Polynomial of a polynomial
The Taylor Polynomial to a function about x=a is a polynomial expressed in powers of (x-a). This example is from Chapter 4 Problem 4a,b in the MATH1231/1241 Calculus notes. Presented by Dr Daniel Mansfield from the UNSW School of Mathematics and Statistics.
From playlist Mathematics 1B (Calculus)

Visual Group Theory, Lecture 6.3: Polynomials and irreducibility
Visual Group Theory, Lecture 6.3: Polynomials and irreducibility A complex number is algebraic over Q (the rationals) if it is the root of a polynomial with rational coefficients. It is clear that every number that can be written with arithmetic and radicals is rational. Galois' big achie
From playlist Visual Group Theory

Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions
Visual Group Theory, Lecture 6.5: Galois group actions and normal field extensions If f(x) has a root in an extension field F of Q, then any automorphism of F permutes the roots of f(x). This means that there is a group action of Gal(f(x)) on the roots of f(x), and this action has only on
From playlist Visual Group Theory

Proof of the existence of the minimal polynomial. Every polynomial that annihilates an operator is a polynomial multiple of the minimal polynomial of the operator. The eigenvalues of an operator are precisely the zeros of the minimal polynomial of the operator.
From playlist Linear Algebra Done Right

A central limit theorem for Gaussian polynomials... pt1 -Anindya De
Anindya De Institute for Advanced Study; Member, School of Mathematics May 13, 2014 A central limit theorem for Gaussian polynomials and deterministic approximate counting for polynomial threshold functions In this talk, we will continue, the proof of the Central Limit theorem from my las
From playlist Mathematics

What is Special About Polynomials? (Perspectives from Coding theory and DiffGeom) - Larry Guth
What is Special About Polynomials? (Perspectives from Coding theory and Differential Geometry) Larry Guth Massachusetts Institute of Technology March 13, 2013 olynomials are a special class of functions. They are useful in many branches of mathematics, often in problems which don't mention
From playlist Mathematics

The Bernstein Sato polynomial: Introduction
This is the first of three talks about the Bernstein-Sato polynomial. The second talk should appear at https://youtu.be/FAKzbvDm-w0 on Dec 22 5:00am PST We define the Bernstein-Sato polynomial of a polynomial in several complex variables, and show how it can be used to analytically con
From playlist Commutative algebra

Visual Group Theory, Lecture 6.4: Galois groups
Visual Group Theory, Lecture 6.4: Galois groups The Galois group Gal(f(x)) of a polynomial f(x) is the automorphism group of its splitting field. The degree of a chain of field extensions satisfies a "tower law", analogous to the tower law for the index of a chain of subgroups. This hints
From playlist Visual Group Theory

New Locally Decodable Codes from Lifting - Madhu Sudan
Madhu Sudan Microsoft Research March 25, 2013 Locally decodable codes (LDCs) are error-correcting codes that allow for highly-efficient recovery of "pieces" of information even after arbitrary corruption of a codeword. Locally testable codes (LTCs) are those that allow for highly-efficient
From playlist Mathematics

Valentin Blomer: The polynomial method for point counting and exponential sums, Lecture 1
We show how families of auxiliary polynomials can be used to count the number of points on certain types of curves over finite fields and to estimate exponential sums and character sums.
From playlist Harmonic Analysis and Analytic Number Theory
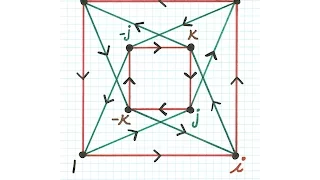
Euler's Formula for the Quaternions
In this video, we will derive Euler's formula using a quaternion power, instead of a complex power, which will allow us to calculate quaternion exponentials such as e^(i+j+k). If you like quaternions, this is a pretty neat formula and a simple generalization of Euler's formula for complex
From playlist Math