
Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions

The Composition of Injective(one-to-one) Functions is Injective Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that the composition of injective(one-to-one) functions is also injective(one-to-one)
From playlist Proofs

Galois theory: Separable extensions
This lecture is part of an online graduate course on Galois theory. We define separable algebraic extensions, and give some examples of separable and non-separable extensions. At the end we briefly discuss purely inseparable extensions.
From playlist Galois theory

CTNT 2020 - Curves over Finite Fields (by Soumya Sankar) - Lecture 4
The Connecticut Summer School in Number Theory (CTNT) is a summer school in number theory for advanced undergraduate and beginning graduate students, to be followed by a research conference. For more information and resources please visit: https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2020 - Curves over Finite Fields (by Soumya Sankar)

How to Prove a Function is Injective(one-to-one) Using the Definition
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to prove a function is injective. Injective functions are also called one-to-one functions. This is a short video focusing on the proof.
From playlist Proofs

Pushing back the barrier of imperfection - F-V. Kuhlmann - Workshop 2 - CEB T1 2018
Franz-Viktor Kuhlmann (Szczecin) / 06.03.2018 The word “imperfection” in our title not only refers to fields that are not perfect, but also to the defect of valued field extensions. The latter is not necessarily directly connected with imperfect fields but may always appear when at least
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

Perfect points on abelian varieties in positive characteristic. - Rössler - Workshop 2 - CEB T2 2019
Damian Rössler (University of Oxford) / 24.06.2019 Perfect points on abelian varieties in positive characteristic. Let K be the function field over a smooth curve over a perfect field of characteristic p 0. Let Kperf be the maximal purely inseparable extension of K. Let A be an abelian
From playlist 2019 - T2 - Reinventing rational points
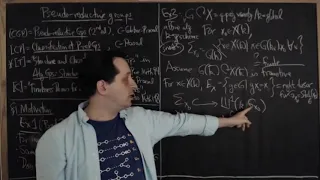
Pseudo-reductive groups by Brian Conrad
PROGRAM ZARISKI-DENSE SUBGROUPS AND NUMBER-THEORETIC TECHNIQUES IN LIE GROUPS AND GEOMETRY (ONLINE) ORGANIZERS: Gopal Prasad, Andrei Rapinchuk, B. Sury and Aleksy Tralle DATE: 30 July 2020 VENUE: Online Unfortunately, the program was cancelled due to the COVID-19 situation but it will
From playlist Zariski-dense Subgroups and Number-theoretic Techniques in Lie Groups and Geometry (Online)

Injective, Surjective and Bijective Functions (continued)
This video is the second part of an introduction to the basic concepts of functions. It looks at the different ways of representing injective, surjective and bijective functions. Along the way I describe a neat way to arrive at the graphical representation of a function.
From playlist Foundational Math

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

👉 Learn how to subtract polynomials. To subtract polynomials, we first simplify the polynomials by removing all brackets. Then, we combine like terms. Like terms are terms that share the same base and power for each variable. When you have identified the like terms, we then apply the requ
From playlist How to subtract polynomials

Irene Bouw, Belyi maps in positive characteristic
VaNTAGe seminar, September 28, 2021 License: CC-BY-NC-SA
From playlist Belyi maps and Hurwitz spaces

A Semistable Model for the Tower of Modular Cures - Jared Weinstein
Jared Weinstein Institute for Advanced Study October 27, 2010 The usual Katz-Mazur model for the modular curve X(pn)X(pn) has horribly singular reduction. For large n there isn't any model of X(pn)X(pn) which has good reduction, but after extending the base one can at least find a semista
From playlist Mathematics

Prove or Disprove if the Function is Injective
Prove or Disprove if the Function is Injective If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Functions, Sets, and Relations

Elliptic Curves - Lecture 5c - Ramification
This video is part of a graduate course on elliptic curves that I taught at UConn in Spring 2021. The course is an introduction to the theory of elliptic curves. More information about the course can be found at the course website: https://alozano.clas.uconn.edu/math5020-elliptic-curves/
From playlist An Introduction to the Arithmetic of Elliptic Curves

Galois theory: Transcendental extensions
This lecture is part of an online graduate course on Galois theory. We describe transcendental extension of fields and transcendence bases. As applications we classify algebraically closed fields and show hw to define the dimension of an algebraic variety.
From playlist Galois theory
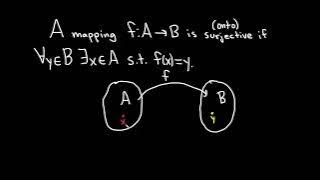
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions

How do we multiply polynomials
👉 Learn how to multiply polynomials. To multiply polynomials, we use the distributive property. The distributive property is essential for multiplying polynomials. The distributive property is the use of each term of one of the polynomials to multiply all the terms of the other polynomial.
From playlist How to Multiply Polynomials

On the notion of genus for division algebras and algebraic groups - Andrei Rapinchu
Joint IAS/Princeton University Number Theory Seminar Topic: On the notion of genus for division algebras and algebraic groups Speaker: Andrei Rapinchu Affiliation: University of Virginia Date: November 2, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions