
A graphical representation of cosets using Caley tables, gives us a deeper insight. In this video we explore two cases. In the first, the element of G that creates the coset of the subgroup is in the subgroup and in the second, it is not.
From playlist Abstract algebra

Sets might contain an element that can be identified as an identity element under some binary operation. Performing the operation between the identity element and any arbitrary element in the set must result in the arbitrary element. An example is the identity element for the binary opera
From playlist Abstract algebra

In this video I do an example problem calculating the right coset of a set, H, with an element from the symmetric group on four elements.
From playlist Abstract algebra

Abstract Algebra | Coset equality.
We present a result which determines when cosets of a subgroup are equal. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

A set might contain many inverse elements under some binary operation. To have such an element, this set must also contain an identity element under the binary operation in question. An element is an inverse element of another element in a set if performing the binary operation between t
From playlist Abstract algebra

In this first video on cosets, I show you the equivalence relation on a group, G, that will turn out to create equivalence classes, which are actually cosets. We will prove later that these equivalence classes created by an element in the group, G, are equal to the set of element made up
From playlist Abstract algebra

The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra

Cyclic groups are first and foremost, as the term implies, groups. What makes them cyclic is that at least on of the elements in the set that makes up the group under a specific binary operation can generate the group by performing the binary operation on itself. So, if a is an element o
From playlist Abstract algebra

Lie groups: Baker Campbell Hausdorff formula
This lecture is part of an online graduate course on Lie groups. We state the Baker Campbell Hausdorff formula for exp(A)exp(B). As applications we show that a Lie group is determined up to local isomorphism by its Lie algebra, and homomorphisms from a simply connected Lie group are deter
From playlist Lie groups

Stable Homotopy Seminar, 21: Computing Homotopy Groups with the Adams Spectral Sequence (Zach Himes)
Zachary Himes constructs the May spectral sequence, a tool using a filtration of of the dual Steenrod algebra that calculates the E2 page of the Adams spectral sequence. May's original insight was that the associated graded of the dual Steenrod algebra is a primitively generated Hopf algeb
From playlist Stable Homotopy Seminar

Daniel Isaksen - 2/3 Motivic and Equivariant Stable Homotopy Groups
Notes: https://nextcloud.ihes.fr/index.php/s/EyZRRtDq965o6WC I will discuss a program for computing C2-equivariant, ℝ-motivic, ℂ-motivic, and classical stable homotopy groups, emphasizing the connections and relationships between the four homotopical contexts. The Adams spectral sequence
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Loïc FOISSY - Cointeracting Bialgebras
Pairs of cointeracting bialgebras recently appears in the literature of combinatorial Hopf algebras, with examples based on formal series, on trees (Calaque, Ebrahimi-Fard, Manchon), graphs (Manchon), posets... We will give several results obtained on pairs of cointeracting bialgebras: act
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Theory of numbers: Congruences: Primitive roots
This lecture is part of an online undergraduate course on the theory of numbers. We define primitive roots, and show that all primes have primitive roots. Correction: At 16:00 two of the square roots of 1 should be (2^k)/2 +1, (2^k)/2-1, not 2^k/2, -2^k/2. For the other lectures in th
From playlist Theory of numbers

David Helm: Whittaker models, converse theorems, and the local Langlands correspondence for ...
Find other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, bibliographies,
From playlist Algebraic and Complex Geometry
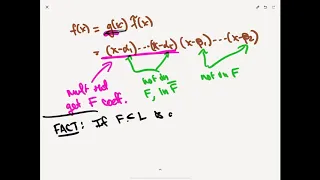
Field Theory - (optional) Primitive Element Theorem - Lecture 15
For finite extensions L \supset F we show that there exists an element \gamma in L such that F(\gamma) = L. This is called the primitive element theorem.
From playlist Field Theory

Lie groups: Poincare-Birkhoff-Witt theorem
This lecture is part of an online graduate course on Lie groups. We state the Poincare-Birkhoff Witt theorem, which shows that the universal enveloping algebra (UEA) of a Lie algebra is the same size as a polynomial algebra. We prove it for Lie algebras of Lie groups and sketch a proof of
From playlist Lie groups

Modular Inverses, Generators, and Order: Linking Elementary Number Theory and Abstract Algebra
Solution to the unique number question posed at 5:01 We show two solution: one is more informal using intuition, and the other using congruences 1) Using Intuition We use a proof by contradiction: suppose that you can reach the same number twice WITHOUT first cycling back to 0. But since y
From playlist Summer of Math Exposition Youtube Videos

Regular permutation groups and Cayley graphs
Cheryl Praeger (University of Western Australia). Plenary Lecture from the 1st PRIMA Congress, 2009. Plenary Lecture 11. Abstract: Regular permutation groups are the 'smallest' transitive groups of permutations, and have been studied for more than a century. They occur, in particular, as
From playlist PRIMA2009

Walter Van SUIJLEKOM - Renormalization Hopf Algebras and Gauge Theories
We give an overview of the Hopf algebraic approach to renormalization, with a focus on gauge theories. We illustrate this with Kreimer's gauge theory theorem from 2006 and sketch a proof. It relates Hopf ideals generated by Slavnov-Taylor identities to the Hochschild cocycles that are give
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Galois theory: Primitive elements
This lecture is part of an online graduate course on Galois theory. We show that any finite separable extension of fields has a primitive element (or generator) and given n example of a finite non-separable extension with no primitive elements.
From playlist Galois theory