
Ex: Determine the Reciprocal of Integers, Fractions, and Mixed Numbers
This video explains how to determine the reciprocal of various rational numbers.
From playlist Multiplying and Dividing Fractions
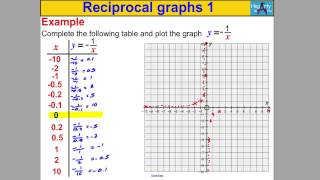
Powered by https://www.numerise.com/ Reciprocal graphs 1
From playlist Important graphs

Find the Reciprocal of a Square root of a Fraction
#shorts This video explains how to determine the reciprocal of the square root of a fraction. https://mathispower4u.com
From playlist Math Shorts

Multiplicative Inverse and Reciprocals
http://www.youtube.com/view_play_list?p=8E39E839B4C6B1DE
From playlist Common Core Standards - 6th Grade

Why did they prove this amazing theorem in 200 different ways? Quadratic Reciprocity MASTERCLASS
The longest Mathologer video ever, just shy of an hour (eventually it's going to happen :) One video I've been meaning to make for a long, long time. A Mathologerization of the Law of Quadratic Reciprocity. This is another one of my MASTERCLASS videos. The slide show consists of 550 slides
From playlist Recent videos

Prealgebra 3.04e - Reciprocals
A brief introduction to reciprocals: The reciprocal of a number, the reciprocal of a fraction, and the fact that any number multiplied by its reciprocal is 1.
From playlist Prealgebra Chapter 3 (Complete chapter)
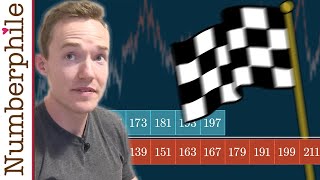
The Prime Number Race (with 3Blue1Brown) - Numberphile
Grant Sanderson discusses a race between two types of prime numbers - and an unexpected result. More links & stuff in full description below ↓↓↓ See all three videos in this series - Grant's Prime Pattern Trilogy: https://bit.ly/PrimePatternTrilogy Grant's own false pattern video: https:
From playlist Prime Pattern Trilogy

This video explains how to determine the prime factorization of a number using a factor tree. http://mathispower4u.yolasite.com/
From playlist Number Sense - Whole Numbers

Ex: Rational Equation App - Find a Number Given the Sum of Reciprocals
This video explains how to solve a number problem given the sum of reciprocals. http://mathispower4u.com
From playlist Solving Applications using Rational Equations

700 years of secrets of the Sum of Sums (paradoxical harmonic series)
Today's video is about the harmonic series 1+1/2+1/3+... . Apart from all the usual bits (done right and animated :) I've included a lot of the amazing properties of this prototypical infinite series that hardly anybody knows about. Enjoy, and if you are teaching this stuff, I hope you'l
From playlist Recent videos

Euler’s Pi Prime Product and Riemann’s Zeta Function
NEW (Christmas 2019). Two ways to support Mathologer Mathologer Patreon: https://www.patreon.com/mathologer Mathologer PayPal: paypal.me/mathologer (see the Patreon page for details) What has pi to do with the prime numbers, how can you calculate pi from the licence plate numbers you en
From playlist Recent videos

"What is the Riemann Hypothesis and why does it matter?" by Ken Ono
The Riemann hypothesis provides insights into the distribution of prime numbers, stating that the nontrivial zeros of the Riemann zeta function have a “real part” of one-half. A proof of the hypothesis would be world news and fetch a $1 million Millennium Prize. In this lecture, Ken Ono wi
From playlist Number Theory Research Unit at CAMS - AUB

Markus Rosenkranz Talk 1 7/8/14 Part 1
Title: A Noncommutative Mikusinski Calculus for Linear Boundary Problems
From playlist Spring 2014

The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis
In this video, I present Euler's proof that the solution to the Basel problem is pi^2/6. I discuss a surprising connection Euler discovered between a generalization of the Basel problem and the Bernoulli numbers, as well as his invention of the zeta function. I explain Euler's discovery of
From playlist Analytic Number Theory

Mitchell Luskin- Electronic Observables for Relaxed 2D van der Waals Heterostructures at Moiré Scale
Recorded 30 March 2022. Mitchell Luskin of the University of Minnesota, Twin Cities, presents "Electronic Observables for Relaxed 2D van der Waals Heterostructures at the Moiré Scale" at IPAM's Multiscale Approaches in Quantum Mechanics Workshop. Abstract: Many novel 2D structures that can
From playlist 2022 Multiscale Approaches in Quantum Mechanics Workshop

Fields Medal Lecture: Cohomology of arithmetic groups — Akshay Venkatesh — ICM2018
Cohomology of arithmetic groups Akshay Venkatesh Abstract: The topology of “arithmetic manifolds”, such as the space of lattices in Rn modulo rotations, encodes subtle arithmetic features of algebraic varieties. In some cases, this can be explained because the arithmetic manifold itself c
From playlist Special / Prizes Lectures

Introduction to number theory lecture 2: Survey.
This lecture is part of my Berkeley math 115 course "Introduction to number theory" We continue the survey of some problems in number theory, and discuss congruences, quadratic reciprocity, additive number theory, recreational number theory, and partitions. For the other lectures in the
From playlist Introduction to number theory (Berkeley Math 115)

MegaFavNumbers: Plus One Primes, 154,641,337, and 62,784,382,823
My entry in the #MegaFavNumbers series looks at a particularly striking example of a very specific family of primes -- and how it connects to what digits can be the final digit of primes in different bases.
From playlist MegaFavNumbers

