Permutations | Factorial and binomial topics
Permutation
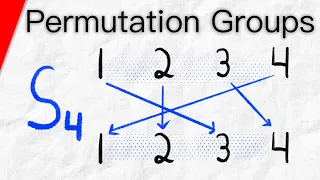
In mathematics, a permutation of a set is, loosely speaking, an arrangement of its members into a sequence or linear order, or if the set is already ordered, a rearrangement of its elements. The word "permutation" also refers to the act or process of changing the linear order of an ordered set. Permutations differ from combinations, which are selections of some members of a set regardless of order. For example, written as tuples, there are six permutations of the set {1, 2, 3}, namely (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), and (3, 2, 1). These are all the possible orderings of this three-element set. Anagrams of words whose letters are different are also permutations: the letters are already ordered in the original word, and the anagram is a reordering of the letters. The study of permutations of finite sets is an important topic in the fields of combinatorics and group theory. Permutations are used in almost every branch of mathematics, and in many other fields of science. In computer science, they are used for analyzing sorting algorithms; in quantum physics, for describing states of particles; and in biology, for describing RNA sequences. The number of permutations of n distinct objects is n factorial, usually written as n!, which means the product of all positive integers less than or equal to n. Technically, a permutation of a set S is defined as a bijection from S to itself. That is, it is a function from S to S for which every element occurs exactly once as an image value. This is related to the rearrangement of the elements of S in which each element s is replaced by the corresponding f(s). For example, the permutation (3, 1, 2) mentioned above is described by the function defined as . The collection of all permutations of a set form a group called the symmetric group of the set. The group operation is the composition (performing two given rearrangements in succession), which results in another rearrangement. As properties of permutations do not depend on the nature of the set elements, it is often the permutations of the set that are considered for studying permutations. In elementary combinatorics, the k-permutations, or partial permutations, are the ordered arrangements of k distinct elements selected from a set. When k is equal to the size of the set, these are the permutations of the set. (Wikipedia).