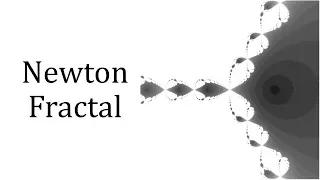
Newton fractal
The Newton fractal is a boundary set in the complex plane which is characterized by Newton's method applied to a fixed polynomial p(Z) ∈ ℂ[Z] or transcendental function. It is the Julia set of the meromorphic function z ↦ z − p(z)/p′(z) which is given by Newton's method. When there are no attractive cycles (of order greater than 1), it divides the complex plane into regions Gk, each of which is associated with a root ζk of the polynomial, k = 1, …, deg(p). In this way the Newton fractal is similar to the Mandelbrot set, and like other fractals it exhibits an intricate appearance arising from a simple description. It is relevant to numerical analysis because it shows that (outside the region of quadratic convergence) the Newton method can be very sensitive to its choice of start point. Almost all points of the complex plane are associated with one of the deg(p) roots of a given polynomial in the following way: the point is used as starting value z0 for Newton's iteration zn + 1 := zn − p(zn)/p'(zn), yielding a sequence of points z1, z2, …, If the sequence converges to the root ζk, then z0 was an element of the region Gk. However, for every polynomial of degree at least 2 there are points for which the Newton iteration does not converge to any root: examples are the boundaries of the basins of attraction of the various roots. There are even polynomials for which open sets of starting points fail to converge to any root: a simple example is z3 − 2z + 2, where some points are attracted by the cycle 0, 1, 0, 1… rather than by a root. An open set for which the iterations converge towards a given root or cycle (that is not a fixed point), is a Fatou set for the iteration. The complementary set to the union of all these, is the Julia set. The Fatou sets have common boundary, namely the Julia set. Therefore, each point of the Julia set is a point of accumulation for each of the Fatou sets. It is this property that causes the fractal structure of the Julia set (when the degree of the polynomial is larger than 2). To plot images of the fractal, one may first choose a specified number d of complex points (ζ1, …, ζd) and compute the coefficients (p1, …, pd) of the polynomial . Then for a rectangular lattice of points in ℂ, one finds the index k(m,n) of the corresponding root ζk(m,n) and uses this to fill an M × N raster grid by assigning to each point (m,n) a color fk(m,n). Additionally or alternatively the colors may be dependent on the distance D(m,n), which is defined to be the first value D such that |zD − ζk(m,n)| < ε for some previously fixed small ε > 0. (Wikipedia).