Measure of non-compactness

Functional analysis

In functional analysis, two measures of non-compactness are commonly used; these associate numbers to sets in such a way that compact sets all get the measure 0, and other sets get measures that are bigger according to "how far" they are removed from compactness. The underlying idea is the following: a bounded set can be covered by a single ball of some radius. Sometimes several balls of a smaller radius can also cover the set. A compact set in fact can be covered by finitely many balls of arbitrary small radius, because it is totally bounded. So one could ask: what is the smallest radius that allows to cover the set with finitely many balls? Formally, we start with a metric space M and a subset X. The ball measure of non-compactness is defined as α(X) = inf {r > 0 : there exist finitely many balls of radius r which cover X} and the Kuratowski measure of non-compactness is defined as β(X) = inf {d > 0 : there exist finitely many sets of diameter at most d which cover X} Since a ball of radius r has diameter at most 2r, we have α(X) ≤ β(X) ≤ 2α(X). The two measures α and β share many properties, and we will use γ in the sequel to denote either one of them. Here is a collection of facts: * X is bounded if and only if γ(X) < ∞. * γ(X) = γ(Xcl), where Xcl denotes the closure of X. * If X is compact, then γ(X) = 0. Conversely, if γ(X) = 0 and X is complete, then X is compact. * γ(X ∪ Y) = max(γ(X), γ(Y)) for any two subsets X and Y. * γ is continuous with respect to the Hausdorff distance of sets. Measures of non-compactness are most commonly used if M is a normed vector space. In this case, we have in addition: * γ(aX) = |a| γ(X) for any scalar a * γ(X + Y) ≤ γ(X) + γ(Y) * γ(conv(X)) = γ(X), where conv(X) denotes the convex hull of X Note that these measures of non-compactness are useless for subsets of Euclidean space Rn: by the Heine–Borel theorem, every bounded closed set is compact there, which means that γ(X) = 0 or ∞ according to whether X is bounded or not. Measures of non-compactness are however useful in the study of infinite-dimensional Banach spaces, for example. In this context, one can prove that any ball B of radius r has α(B) = r and β(B) = 2r. (Wikipedia).

Math 101 Fall 2017 112917 Introduction to Compact Sets

Definition of an open cover. Definition of a compact set (in the real numbers). Examples and non-examples. Properties of compact sets: compact sets are bounded. Compact sets are closed. Closed subsets of compact sets are compact. Infinite subsets of compact sets have accumulation poi

From playlist Course 6: Introduction to Analysis (Fall 2017)

Math 101 Introduction to Analysis 112515: Introduction to Compact Sets

Introduction to Compact Sets: open covers; examples of finite and infinite open covers; definition of compactness; example of a non-compact set; compact implies closed; closed subset of compact set is compact; continuous image of a compact set is compact

From playlist Course 6: Introduction to Analysis

Math 101 Introduction to Analysis 113015: Compact Sets, ct'd

Compact sets, continued. Recalling various facts about compact sets. Compact implies infinite subsets have limit points (accumulation points), that is, compactness implies limit point compactness; collections of compact sets with the finite intersection property have nonempty intersectio

From playlist Course 6: Introduction to Analysis

Topology: Compactness

This video is about compactness and some of its basic properties.

From playlist Basics: Topology

Math 131 092816 Continuity; Continuity and Compactness

Review definition of limit. Definition of continuity at a point; remark about isolated points; connection with limits. Composition of continuous functions. Alternate characterization of continuous functions (topological definition). Continuity and compactness: continuous image of a com

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Math 131 Fall 2018 100118 Properties of Compact Sets

Review of compactness. Properties: compactness is not relative. Compact implies closed. Closed subset of compact set is compact. [Infinite] Collection of compact sets with finite intersection property has a nonempty intersection.

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Maximum and Minimum

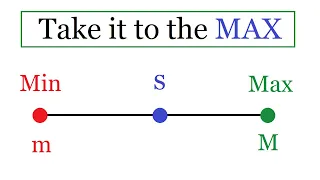
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh

From playlist Real Numbers

Math 131 Fall 2018 100318 Heine Borel Theorem

Definition of limit point compactness. Compact implies limit point compact. A nested sequence of closed intervals has a nonempty intersection. k-cells are compact. Heine-Borel Theorem: in Euclidean space, compactness, limit point compactness, and being closed and bounded are equivalent

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

Properties of Compactness

Compact sets enjoy some mysterious properties, which I'll discuss in this video. More precisely, compact sets are always bounded and closed. The beauty of this result lies in the proof, which is an elegant application of this subtle concept. Enjoy! Compactness Definition: https://youtu.be

From playlist Topology

Matthew Kennedy: Noncommutative convexity

Talk by Matthew Kennedy in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on May 5, 2021

From playlist Global Noncommutative Geometry Seminar (Europe)

H-measure and Applications by M Vanninathan

PROGRAM: MULTI-SCALE ANALYSIS AND THEORY OF HOMOGENIZATION ORGANIZERS: Patrizia Donato, Editha Jose, Akambadath Nandakumaran and Daniel Onofrei DATE: 26 August 2019 to 06 September 2019 VENUE: Madhava Lecture Hall, ICTS, Bangalore Homogenization is a mathematical procedure to understa

From playlist Multi-scale Analysis And Theory Of Homogenization 2019

A nonabelian Brunn-Minkowski inequality - Ruixiang Zhang

Members’ Seminar Topic: A nonabelian Brunn-Minkowski inequality Speaker: Ruixiang Zhang Affiliation: University of Wisconsin-Madison; Member, School of Mathematics Date: January 25, 2021 For more video please visit http://video.ias.edu

From playlist Mathematics

Lyapunov exponents of probability distributions....by Adriana Sanchez Chavarria

PROGRAM SMOOTH AND HOMOGENEOUS DYNAMICS ORGANIZERS: Anish Ghosh, Stefano Luzzatto and Marcelo Viana DATE: 23 September 2019 to 04 October 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Ergodic theory has its origins in the the work of L. Boltzmann on the kinetic theory of gases.

From playlist Smooth And Homogeneous Dynamics

Intrinsic Diophantine approximation (Lecture 1) by Amos Nevo

From playlist Smooth And Homogeneous Dynamics

The Embedding Problem of Infinitely Divisible Probability Measures on Groups by Riddhi Shah

PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis

From playlist Ergodic Theory and Dynamical Systems 2022

The Abel lectures: Hillel Furstenberg and Gregory Margulis

0:30 Welcome by Hans Petter Graver, President of the Norwegian Academy of Science Letters 01:37 Introduction by Hans Munthe-Kaas, Chair of the Abel Prize Committee 04:16 Hillel Furstenberg: Random walks in non-euclidean space and the Poisson boundary of a group 58:40 Questions and answers

From playlist Gregory Margulis

Asymptotic invariants of locally symmetric spaces – Tsachik Gelander – ICM2018

Lie Theory and Generalizations Invited Lecture 7.4 Asymptotic invariants of locally symmetric spaces Tsachik Gelander Abstract: The complexity of a locally symmetric space M is controlled by its volume. This phenomena can be measured by studying the growth of topological, geometric, alge

From playlist Lie Theory and Generalizations

Uri Bader - 2/4 Algebraic Representations of Ergodic Actions

Ergodic Theory is a powerful tool in the study of linear groups. When trying to crystallize its role, emerges the theory of AREAs, that is Algebraic Representations of Ergodic Actions, which provides a categorical framework for various previously studied concepts and methods. Roughly, this

From playlist Uri Bader - Algebraic Representations of Ergodic Actions

Dustin Clausen: New foundations for functional analysis

Talk by Dustin Clausen in Global Noncommutative Geometry Seminar (Americas) on November 12, 2021.

From playlist Global Noncommutative Geometry Seminar (Americas)

Math 131 092116 Properties of Compact Sets

Properties of compact sets. Compact implies closed; closed subsets of compact sets are compact; collections of compact sets that satisfy the finite intersection property have a nonempty intersection; infinite subsets of compact sets must have a limit point; the infinite intersection of ne

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Measure of non-compactness

Related pages