
(ML 14.2) Markov chains (discrete-time) (part 1)
Definition of a (discrete-time) Markov chain, and two simple examples (random walk on the integers, and a oversimplified weather model). Examples of generalizations to continuous-time and/or continuous-space. Motivation for the hidden Markov model.
From playlist Machine Learning

(ML 14.3) Markov chains (discrete-time) (part 2)
Definition of a (discrete-time) Markov chain, and two simple examples (random walk on the integers, and a oversimplified weather model). Examples of generalizations to continuous-time and/or continuous-space. Motivation for the hidden Markov model.
From playlist Machine Learning
(ML 14.1) Markov models - motivating examples
Introduction to Markov models, using intuitive examples of applications, and motivating the concept of the Markov chain.
From playlist Machine Learning
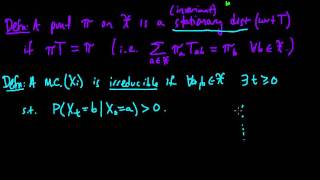
(ML 18.3) Stationary distributions, Irreducibility, and Aperiodicity
Definitions of the properties of Markov chains used in the Ergodic Theorem: time-homogeneous MC, stationary distribution of a MC, irreducible MC, aperiodic MC.
From playlist Machine Learning

Prob & Stats - Markov Chains (8 of 38) What is a Stochastic Matrix?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a stochastic matrix. Next video in the Markov Chains series: http://youtu.be/YMUwWV1IGdk
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

(ML 18.4) Examples of Markov chains with various properties (part 1)
A very simple example of a Markov chain with two states, to illustrate the concepts of irreducibility, aperiodicity, and stationary distributions.
From playlist Machine Learning

Diophantine properties of Markoff numbers - Jean Bourgain
Using available results on the strong approximation property for the set of Markoff triples together with an extension of Zagier’s counting result, we show that most Markoff numbers are composite. For more videos, visit http://video.ias.edu
From playlist Mathematics

Intro to Markov Chains & Transition Diagrams
Markov Chains or Markov Processes are an extremely powerful tool from probability and statistics. They represent a statistical process that happens over and over again, where we try to predict the future state of a system. A markov process is one where the probability of the future ONLY de
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)

Prob & Stats - Markov Chains (9 of 38) What is a Regular Matrix?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a regular matrix. Next video in the Markov Chains series: http://youtu.be/loBUEME5chQ
From playlist iLecturesOnline: Probability & Stats 3: Markov Chains & Stochastic Processes

Probability - Convergence Theorems for Markov Chains: Oxford Mathematics 2nd Year Student Lecture:
These lectures are taken from Chapter 6 of Matthias Winkel’s Second Year Probability course. Their focus is on the main convergence theorems of Markov chains. You can watch many other student lectures via our main Student Lectures playlist (also check out specific student lectures playlis
From playlist Oxford Mathematics Student Lectures - Probability

(ML 18.2) Ergodic theorem for Markov chains
Statement of the Ergodic Theorem for (discrete-time) Markov chains. This gives conditions under which the average over time converges to the expected value, and under which the marginal distributions converge to the stationary distribution.
From playlist Machine Learning

Cécile Mailler : Processus de Pólya à valeur mesure
Résumé : Une urne de Pólya est un processus stochastique décrivant la composition d'une urne contenant des boules de différentes couleurs. L'ensemble des couleurs est usuellement un ensemble fini {1, ..., d}. A chaque instant n, une boule est tirée uniformément au hasard dans l'urne (noton
From playlist Probability and Statistics

Equidistribution of Measures with High Entropy for General Surface Diffeomorphisms by Omri Sarig
PROGRAM : ERGODIC THEORY AND DYNAMICAL SYSTEMS (HYBRID) ORGANIZERS : C. S. Aravinda (TIFR-CAM, Bengaluru), Anish Ghosh (TIFR, Mumbai) and Riddhi Shah (JNU, New Delhi) DATE : 05 December 2022 to 16 December 2022 VENUE : Ramanujan Lecture Hall and Online The programme will have an emphasis
From playlist Ergodic Theory and Dynamical Systems 2022

Regenerative Stochastic Processes by Krishna Athreya
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Experimentation with Temporal Interference: by Peter W Glynn
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Regenerative sequences and processes and MCMC by Krishna Athreya
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Marek Biskup: Extreme points of two dimensional discrete Gaussian free field part 3
This lecture was held during winter school (01.19.2015 - 01.23.2015)
From playlist HIM Lectures 2015

Diophantine Analysis of affine cubic Markoff type Surfaces - Peter Sarnak
Speaker: Peter Sarnak (Princeton/IAS) Title: Diophantine Analysis of affine cubic Markoff type Surfaces More videos on http://video.ias.edu
From playlist Mathematics

Hamza Fawzi: "Sum-of-squares proofs of logarithmic Sobolev inequalities on finite Markov chains"
Entropy Inequalities, Quantum Information and Quantum Physics 2021 "Sum-of-squares proofs of logarithmic Sobolev inequalities on finite Markov chains" Hamza Fawzi - University of Cambridge Abstract: Logarithmic Sobolev inequalities play an important role in understanding the mixing times
From playlist Entropy Inequalities, Quantum Information and Quantum Physics 2021

MIT 6.262 Discrete Stochastic Processes, Spring 2011 View the complete course: http://ocw.mit.edu/6-262S11 Instructor: Robert Gallager License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 6.262 Discrete Stochastic Processes, Spring 2011