
Proof of the Dot Product Theorem
Dot products are essential in a mathematician's toolbox. There is a property of dot products, however, that is often taken for granted: the multiplication of the magnitudes of two vectors by the cosine of the angle between them equals the sum of the multiplication of their respective compo
From playlist Fun

In this video I write down the axioms of Lie algebras and then discuss the defining anti-symmetric bilinear map (the Lie bracket) which is zero on the diagonal and fulfills the Jacobi identity. I'm following the compact book "Introduction to Lie Algebras" by Erdmann and Wildon. https://gi
From playlist Algebra

Now that we have defined and understand quotient groups, we need to look at product groups. In this video I define the product of two groups as well as the group operation, proving that it is indeed a group.
From playlist Abstract algebra

Inner products (video 3): Definition
Recordings of the corresponding course on Coursera. If you are interested in exercises and/or a certificate, have a look here: https://www.coursera.org/learn/pca-machine-learning
From playlist Inner Products

Lie derivatives of differential forms
Introduces the lie derivative, and its action on differential forms. This is applied to symplectic geometry, with proof that the lie derivative of the symplectic form along a Hamiltonian vector field is zero. This is really an application of the wonderfully named "Cartan's magic formula"
From playlist Symplectic geometry and mechanics

Calculus 3.07e - The Product Rule
The Product Rule for derivatives
From playlist Calculus Ch 3 - Derivatives

This is the third video of a series from the Worldwide Center of Mathematics explaining the basics of vectors. This video explains the precise definition of dot product (also known as scalar product) and shows some examples of calculated dot products. For more math videos, visit our channe
From playlist Basics: Vectors

This lecture is part of an online graduate course on Lie groups. We define the Lie algebra of a Lie group in two ways, and show that it satisfied the Jacobi identity. The we calculate the Lie algebras of a few Lie groups. For the other lectures in the course see https://www.youtube.co
From playlist Lie groups

What is the formula for the dot product
http://www.freemathvideos.com In this video series I will show you how to apply the dot product of two vectors and use the product to determine if two vectors are orthogonal or not. The dot product does not produce another vector like scalar multiplication but rather produces a scalar tha
From playlist Vectors

Lie groups: Baker Campbell Hausdorff formula
This lecture is part of an online graduate course on Lie groups. We state the Baker Campbell Hausdorff formula for exp(A)exp(B). As applications we show that a Lie group is determined up to local isomorphism by its Lie algebra, and homomorphisms from a simply connected Lie group are deter
From playlist Lie groups

Lie Groups and Lie Algebras: Lesson 25 - the commutator and the Lie Algebra
Lie Groups and Lie Algebras: Lesson 25 - the commutator In this lecture we discover how to represent an infinitesimal commutator of the Lie group using a member of the Lie algebra. We promote the vector space spawned by the group generators to an algebra. Please consider supporting this
From playlist Lie Groups and Lie Algebras

Mod-01 Lec-19 Linear Least Square Estimation and Geometric Interpretation
Advanced Numerical Analysis by Prof. Sachin C. Patwardhan,Department of Chemical Engineering,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Bombay: Advanced Numerical Analysis | CosmoLearning.org

Jon Keating: Random matrices, integrability, and number theory - Lecture 1
Abstract: I will give an overview of connections between Random Matrix Theory and Number Theory, in particular connections with the theory of the Riemann zeta-function and zeta functions defined in function fields. I will then discuss recent developments in which integrability plays an imp
From playlist Analysis and its Applications
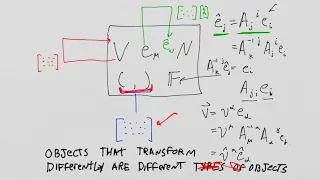
Lie Groups and Lie Algebras: Lesson 7 - The Classical Groups Part V
Lie Groups and Lie Algebras: Lesson 7 - The Classical Groups Part V We discuss the matrix interpretation of the metric even more, since it is critical to our understanding of the classical groups. Please consider supporting this channel via Patreon: https://www.patreon.com/XYLYXYLYX
From playlist Lie Groups and Lie Algebras

Cross product and area of parallelogram
How to compute area of parallelogram via cross products of vectors. Free ebook https://bookboon.com/en/introduction-to-vectors-ebook (updated link) Test your understanding via a short quiz http://goo.gl/forms/v8utjHDRT3
From playlist Introduction to Vectors

Jean Michel BISMUT - Fokker-Planck Operators and the Center of the Enveloping Algebra
The heat equation method in index theory gives an explicit local formula for the index of a Dirac operator. Its Lagrangian counterpart involves supersymmetric path integrals. Similar methods can be developed to give a geometric formula for semi simple orbital integrals associated with the
From playlist Integrability, Anomalies and Quantum Field Theory

Kannan Soundararajan - Selberg's Contributions to the Theory of Riemann Zeta Function [2008]
http://www.ams.org/notices/200906/rtx090600692p-corrected.pdf January 11, 2008 3:00 PM Peter Goddard, Director Welcome Kannan Soundararajan Selberg's Contributions to the Theory of Riemann Zeta Function and Dirichlet L-Functions Atle Selberg Memorial Memorial Program in Honor of His
From playlist Number Theory

Halting Problem & Quantum Entanglement 2020 Breakthrough result [MIP*=RE]
This video explains the MIP*=RE result. We skip the proof details, just explain what the result means. Please leave comments in the comment section if something is unclear. The links mentioned in the video: 1) Proof that the halting problem can't be solved: https://youtu.be/92WHN-pAFCs
From playlist Animated Physics Simulations

The KPZ fixed point - (Lecture 4) by Daniel Remenik
PROGRAM :UNIVERSALITY IN RANDOM STRUCTURES: INTERFACES, MATRICES, SANDPILES ORGANIZERS :Arvind Ayyer, Riddhipratim Basu and Manjunath Krishnapur DATE & TIME :14 January 2019 to 08 February 2019 VENUE :Madhava Lecture Hall, ICTS, Bangalore The primary focus of this prog
From playlist Universality in random structures: Interfaces, Matrices, Sandpiles - 2019

The Product Rule of Differentiation (Introduction)
This video is a new version of the introductory video to the product rule of differentiation. Site: http://mathispower4u.com Search: http://mathispower4u.wordpress.com
From playlist Differentiation Using the Product Rule