
Lagrange multipliers: 2 constraints
Free ebook http://tinyurl.com/EngMathYT A lecture showing how to apply the method of Lagrange multipliers where two contraints are involved.
From playlist Lagrange multipliers

Introduction to Euler's Totient Function!
Euler's totient function φ(n) is an important function in number theory. Here we go over the basics of the definition of the totient function as well as the value for prime numbers and powers of prime numbers! Modular Arithmetic playlist: https://www.youtube.com/playlist?list=PLug5ZIRrShJ
From playlist Modular Arithmetic
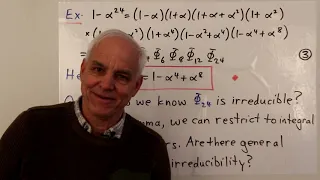
Irreducibility and the Schoenemann-Eisenstein criterion | Famous Math Probs 20b | N J Wildberger
In the context of defining and computing the cyclotomic polynumbers (or polynomials), we consider irreducibility. Gauss's lemma connects irreducibility over the integers to irreducibility over the rational numbers. Then we describe T. Schoenemann's irreducibility criterion, which uses some
From playlist Famous Math Problems

Lagrangian Floer theory in symplectic fibrations - Douglas Schultz
Princeton/IAS Symplectic Geometry Seminar Topic: Lagrangian Floer theory in symplectic fibrations Speaker: Douglas Schultz Affiliation: Rutgers University Date:April 27, 2017 For more info, please visit http://video.ias.edu
From playlist Mathematics

Lehmer Factor Stencils: A paper factoring machine before computers
In 1929, Derrick N. Lehmer published a set of paper stencils used to factor large numbers by hand before the advent of computers. We explain the math behind the stencils, which includes modular arithmetic, quadratic residues, and continued fractions, including my favourite mathematical vi
From playlist Joy of Mathematics

Lagrange multipliers: 2 constraints
Download the free PDF http://tinyurl.com/EngMathYT This video shows how to apply the method of Lagrange multipliers to a max/min problem. Such ideas are seen in university mathematics.
From playlist Several Variable Calculus / Vector Calculus
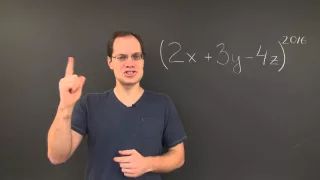
Sum of Polynomial Coefficients Challenge
Solution on Lemma: https://www.lem.ma/-K (and additional challenges) Tangentially related good read: http://bit.ly/PascalsTri Twitter: https://twitter.com/PavelGrinfeld
From playlist Problems, Paradoxes, and Sophisms
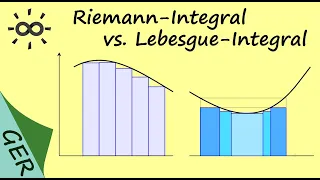
Riemann-Integral vs. Lebesgue-Integral
English version here: https://www.youtube.com/watch?v=PGPZ0P1PJfw Unterstützt den Kanal auf Steady: https://steadyhq.com/en/brightsideofmaths Ihr werdet direkt informiert, wenn ich einen Livestream anbiete. Hier erkläre ich den Unterschied zwischen Riemann-Integral und Lebesgue-Integral
From playlist Analysis

How they found the World's Biggest Prime Number - Numberphile
Featuring Matt Parker... More links & stuff in full description below ↓↓↓ See part one at: https://youtu.be/tlpYjrbujG0 Part three on Numberphile2: https://youtu.be/jNXAMBvYe-Y Matt's interview with Curtis Cooper: https://youtu.be/q5ozBnrd5Zc The previous record: https://youtu.be/QSEKzFG
From playlist Matt Parker (standupmaths) on Numberphile

This lecture is part of an online course on rings and modules. We continue the previous lecture on complete rings by discussing Hensel's lemma for finding roots of polynomials over p-adic rings or over power series rings. We sketch two proofs, by slowly improving a root one digit at a tim
From playlist Rings and modules

Discrete Structures: Multiplicative Inverse; Greatest Common Divisor; Euler's Totient Function
Decrypting the linear cipher leaves us with a fundamental problem: dividing two integers yields a fraction, which is difficult to work with. Learn about new concepts: the greatest common divisor (GCD), the multiplicative inverse, and Euler's totient function. These will allow us to decrypt
From playlist Discrete Structures, Spring 2022

AKPotW: A Lack of Primitive Roots [Number Theory]
If this video is confusing, be sure to check out our blog for the full solution transcript! https://centerofmathematics.blogspot.com/2018/05/advanced-knowledge-problem-of-week-5-3.html
From playlist Center of Math: Problems of the Week
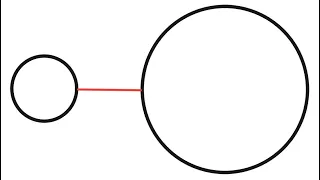
Lagrange multiplier two constraints
In this video, I give an example of Lagrange multipliers with two constraints by calculating the shortest and the longest distance between two disks.
From playlist Partial Derivatives

Discrete Structures: Public Key Cryptography; RSA
See that little "lock" icon in your browser's address bar? What does that mean? Learn about the RSA algorithm, how it helps solve the key-exchange problem, and how your browser uses these algorithms to protect your privacy.
From playlist Discrete Structures, Spring 2022

Discrete Structures: Digital certificates and implementing RSA
Our last session on RSA and public key cryptography. We'll learn about digital certificates and see how to implement the core RSA algorithms in Python.
From playlist Discrete Structures, Spring 2022

Prime Numbers Make the Internet Possible. Here's How - The RSA Encryption Algorithm
In this video I talk about the RSA Encryption Algorithm, and about the history of cryptography. People have been coding and decoding information ever since we learnt how to write. The Romans were one of the first to implement it, making what they considered to be the unbreakable 'Caesar C
From playlist Prime Numbers

GT12. Aut(Z/n) and Fermat's Little Theorem
Abstract Algebra: We show that Aut(Z/n) is isomorphic to (Z/n)*, the group of units in Z/n. In turn, we show that the units consist of all m in Z/n with gcd(m,n)=1. Using (Z/n)*, we define the Euler totient function and state and prove Fermat's Little Theorem: if p is a prime, then, for
From playlist Abstract Algebra

Discrete Structures: Multiplicative inverse, Euler's totient function, and Euler's theorem
This is a continuation of the previous live stream session. Learn more about Euler's totient function and how we can use it, along with Euler's theorem, to compute the multiplicative inverse of any number (a mod n). We'll also learn about the extended Euclidean algorithm to compute the mul
From playlist Discrete Structures, Spring 2022

Proof & Explanation: Gauss's Lemma in Number Theory
Euler's criterion: https://youtu.be/2IBPOI43jek One common proof of quadratic reciprocity uses Gauss's lemma. To understand Gauss's lemma, here we prove how it works using Euler's criterion and the Legendre symbol. Quadratic Residues playlist: https://www.youtube.com/playlist?list=PLug5Z
From playlist Quadratic Residues