
Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)
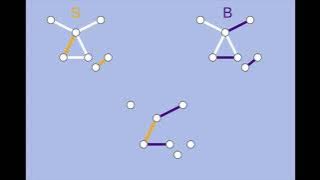
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants
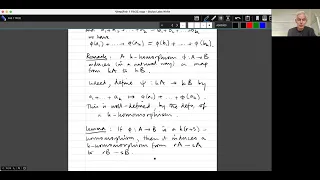
Introduction to additive combinatorics lecture 5.8 --- Freiman homomorphisms and isomorphisms.
The notion of a Freiman homomorphism and the closely related notion of a Freiman isomorphism are fundamental concepts in additive combinatorics. Here I explain what they are and prove a lemma that states that a subset A of F_p^N such that kA - kA is not too large is "k-isomorphic" to a sub
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Bryna Kra : Multiple ergodic theorems: old and new - lecture 2
Abstract : The classic mean ergodic theorem has been extended in numerous ways: multiple averages, polynomial iterates, weighted averages, along with combinations of these extensions. I will give an overview of these advances and the different techniques that have been used, focusing on co
From playlist Dynamical Systems and Ordinary Differential Equations

some2: transforming normals part 3
Some2 submission version Part1 intro: https://youtu.be/BWr0gQoyUEM Part2: concepts and intuitions: https://youtu.be/QLPcBi47Wzk Part 3: this video This is for Some2. #SoME2 #3b1b All the manim source code will be published soon. License: CC BY-NC-SA 2.0
From playlist Summer of Math Exposition 2 videos

Cluster characters, generic bases for cluster algebras (Lecture 4) by Pierre-Guy Plamondon
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

Weil conjectures 1 Introduction
This talk is the first of a series of talks on the Weil conejctures. We recall properties of the Riemann zeta function, and describe how Artin used these to motivate the definition of the zeta function of a curve over a finite field. We then describe Weil's generalization of this to varie
From playlist Algebraic geometry: extra topics

Geometric complexity theory from a combinatorial viewpoint - Greta Panova
Computer Science/Discrete Mathematics Seminar II Topic: Lattices: from geometry to cryptography Speaker: Greta Panova Affiliation: University of Pennsylvania; von Neumann Fellow, School of Mathematics Date: November 28, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics
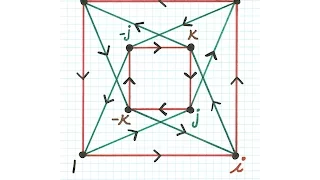
Euler's Formula for the Quaternions
In this video, we will derive Euler's formula using a quaternion power, instead of a complex power, which will allow us to calculate quaternion exponentials such as e^(i+j+k). If you like quaternions, this is a pretty neat formula and a simple generalization of Euler's formula for complex
From playlist Math

49: April Hamilton Jacobi theory - Part 1
Jacob Linder: 12.04.2012, Classical Mechanics (TFY4345), v2012 NTNU A full textbook covering the material in the lectures in detail can be downloaded for free here: http://bookboon.com/en/introduction-to-lagrangian-hamiltonian-mechanics-ebook
From playlist NTNU: TFY 4345 - Classical Mechanics | CosmoLearning Physics

Ch 4: What is an inner product? | Maths of Quantum Mechanics
Hello! This is the fourth chapter in my series "Maths of Quantum Mechanics." In this episode, we'll derive some intuition for the inner product, and understand why it is a useful tool in quantum mechanics. If you have any questions or comments, shoot me an email at: quantumsensechannel@
From playlist Maths of Quantum Mechanics

Introduction to number theory lecture 36 Kronecker symbol
This lecture is part of my Berkeley math 115 course "Introduction to number theory" For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj53L8sMbzIhhXSAOpuZ1Fov8 We define the Kronecker symbol and summarize its properties. The textbook is "An introduc
From playlist Introduction to number theory (Berkeley Math 115)

Bryna Kra : Multiple ergodic theorems: old and new - lecture 3
Abstract : The classic mean ergodic theorem has been extended in numerous ways: multiple averages, polynomial iterates, weighted averages, along with combinations of these extensions. I will give an overview of these advances and the different techniques that have been used, focusing on co
From playlist Dynamical Systems and Ordinary Differential Equations

Asymptotic spectra and Applications I - Jeroen Zuiddam
Computer Science/Discrete Mathematics Seminar I Topic: Asymptotic spectra and Applications I Speaker: Jeroen Zuiddam Affiliation: Member, School of Mathematics Date: October 8, 2019 For more video please visit http://video.ias.edu
From playlist Mathematics

The Campbell-Baker-Hausdorff and Dynkin formula and its finite nature
In this video explain, implement and numerically validate all the nice formulas popping up from math behind the theorem of Campbell, Baker, Hausdorff and Dynkin, usually a.k.a. Baker-Campbell-Hausdorff formula. Here's the TeX and python code: https://gist.github.com/Nikolaj-K/8e9a345e4c932
From playlist Algebra

Tensor Calculus 4c: A Few Tensor Notation Exercises
This course will eventually continue on Patreon at http://bit.ly/PavelPatreon Textbook: http://bit.ly/ITCYTNew Errata: http://bit.ly/ITAErrata McConnell's classic: http://bit.ly/MCTensors Table of Contents of http://bit.ly/ITCYTNew Rules of the Game Coordinate Systems and the Role of Te
From playlist Introduction to Tensor Calculus