
We define the Kantorovich dual of Kantorovich problem of Optimal Transport and give a (well known) interpretation in terms of "outsourcing" the task of transporting goods.
From playlist Optimal Transport
In this video, I state and prove Chebyshev's inequality, and its cousin Markov's inequality. Those inequalities tell us how big an integrable function can really be. Enjoy!
From playlist Real Analysis

Joe Neeman: Gaussian isoperimetry and related topics I
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Joe Neeman: Gaussian isoperimetry and related topics II
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Cauchy Schwarz Inequality I (visual proof)
This is a short, animated visual proof of the two-dimensional Cauchy-Schwarz inequality (sometimes called Cauchy–Bunyakovsky–Schwarz inequality) using the Side-angle-side formula for the area of a parallelogram. #math #inequality #manim #animation #theorem #pww #proofwithoutwords #
From playlist Inequalities

An introduction to the Gromov-Hausdorff distance
Title: An introduction to the Gromov-Hausdorff distance Abstract: We give a brief introduction to the Hausdorff and Gromov-Hausdorff distances between metric spaces. The Hausdorff distance is defined on two subsets of a common metric space. The Gromov-Hausdorff distance is defined on any
From playlist Tutorials
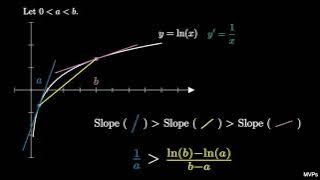
Napier's Inequality (two visual proofs via calculus)
This is two short, animated visual proofs of the Napier's inequality: one using derivatives and one using integrals. This theorem bounds the reciprocal of the logarithm mean. #mathshorts #mathvideo #math #napierinequality #napier #inequality #logarithm #logarithmicmean #manim #animation #t
From playlist Inequalities

Joe Neeman: Gaussian isoperimetry and related topics III
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

Decision Making and Inference Under Model Misspecification by Jose Blanchet
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Robert MacCann - Optimal Transport - Lecture 1
1. Introduction 2. References 1:43 Guillen and MacCann: http://www.math.toronto.edu/mccann/papers/FiveLectures.pdf MacCann: http://www.math.toronto.edu/mccann/papers/glimpse.pdf Chiappori, MacCann and Pass: http://www.math.toronto.edu/mccann/papers/CMPMath.pdf Chiappori, MacCann and Pass:
From playlist 2016 - Calculus of Variations and PDE's

Concentration of quantum states from quantum functional (...) - N. Datta - Workshop 2 - CEB T3 2017
Nilanjana Datta / 24.10.17 Concentration of quantum states from quantum functional and transportation cost inequalities Quantum functional inequalities (e.g. the logarithmic Sobolev- and Poincaré inequalities) have found widespread application in the study of the behavior of primitive q
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Matthias Liero: On entropy transport problems and the Hellinger Kantorovich distance
In this talk, we will present a general class of variational problems involving entropy-transport minimization with respect to a couple of given finite measures with possibly unequal total mass. These optimal entropy-transport problems can be regarded as a natural generalization of classic
From playlist HIM Lectures: Follow-up Workshop to JTP "Optimal Transportation"

Stefano Gualandi: "Discrete Optimal Transport by Parallel Network Simplex"
Deep Learning and Combinatorial Optimization 2021 "Discrete Optimal Transport by Parallel Network Simplex" Stefano Gualandi - Università di Pavia Abstract: We present recent results on the solution of problems related to the theory of Optimal Transport by using an efficient parallel impl
From playlist Deep Learning and Combinatorial Optimization 2021

Z. Badreddine - Optimal transportation problem and MCP property on sub-Riemannian structures
This presentation is devoted to the study of mass transportation on sub-Riemannian geometry. In order to obtain existence and uniqueness of optimal transport maps, the first relevant method to consider is the one used by Figalli and Rifford which is based on the local semiconcavity of the
From playlist Journées Sous-Riemanniennes 2018

Yair Shenfeld - The Brownian transport map - IPAM at UCLA
Recorded 09 February 2022. Yair Shenfeld of the Massachusetts Institute of Technology presents "The Brownian transport map" at IPAM's Calculus of Variations in Probability and Geometry Workshop. Abstract: The existence of Lipschitz transport maps between probability measures leads to tran
From playlist Workshop: Calculus of Variations in Probability and Geometry

To learn more about Wolfram Technology Conference, please visit: https://www.wolfram.com/events/technology-conference/ Speaker: Rob Knapp Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and mor
From playlist Wolfram Technology Conference 2018

Ramon van Handel: The mysterious extremals of the Alexandrov-Fenchel inequality
The Alexandrov-Fenchel inequality is a far-reaching generalization of the classical isoperimetric inequality to arbitrary mixed volumes. It is one of the central results in convex geometry, and has deep connections with other areas of mathematics. The characterization of its extremal bodie
From playlist Trimester Seminar Series on the Interplay between High-Dimensional Geometry and Probability

Thomas Courtade : Information Theoretic Perspective on Brascamp -Lieb- Barthe Inequalities
Recording during the thematic meeting : "Geometrical and Topological Structures of Information" the August 28, 2017 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent
From playlist Geometry

Bernoulli's Inequality (two visual proofs via calculus)
This is two short, animated visual proofs of the Bernoulli's inequality: one using derivatives and one using integrals. #calculus #math #bernoulli #inequality #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #mathvideo #mathematics If you liked this video, please co
From playlist Inequalities