
Universal covering spaces | Algebraic Topology | NJ Wildberger
We begin by giving some examples of the main theorem from the last lecture: that the associated homomorphism of fundamental groups associated to a covering space p:X to B injects pi(X) as a subgroup of pi(B). We look at helical coverings of a circle, and also a two-fold covering of the wed
From playlist Algebraic Topology

Lie groups: Poincare-Birkhoff-Witt theorem
This lecture is part of an online graduate course on Lie groups. We state the Poincare-Birkhoff Witt theorem, which shows that the universal enveloping algebra (UEA) of a Lie algebra is the same size as a polynomial algebra. We prove it for Lie algebras of Lie groups and sketch a proof of
From playlist Lie groups

AlgTop28: Covering spaces and fundamental groups
We illustrate the ideas from the last lectures by giving some more examples of covering spaces: of the torus, and the two-holed torus. Then we begin to explore the relationship between the fundamental groups of a covering space X and a base space B under a covering map p:X to B. For this
From playlist Algebraic Topology

Functional Analysis Lecture 13 2014 03 061 Boundedness of Hilbert Transform on Hardy Space (part 2)
Finishing the proof: going from atoms to Hardy space functions. Hardy space and maximal functions: maximal function associated with a function of compact support; boundedness of such maximal functions from Hardy space into L^1. Functions of bounded mean oscillation (BMO). Basic observat
From playlist Course 9: Basic Functional and Harmonic Analysis

Functional Analysis Lecture 12 2014 03 04 Boundedness of Hilbert Transform on Hardy Space (part 1)
Dyadic Whitney decomposition needed to extend characterization of Hardy space functions to higher dimensions. p-atoms: definition, have bounded Hardy space norm; p-atoms can also be used in place of atoms to define Hardy space. The Hilbert Transform is bounded from Hardy space to L^1: b
From playlist Course 9: Basic Functional and Harmonic Analysis

Functional Analysis Lecture 10 2014 02 20 L^p boundedness of the Maximal Function
Definition of maximal function. Weak-type inequality. Covering lemma. Distribution function of a non-negative measurable function. Tchebychev’s inequality. Proof of boundedness of the maximal function via interpolation. Atomic Decomposition of Hardy space H_r^1: definition of atoms;
From playlist Course 9: Basic Functional and Harmonic Analysis

Joe Neeman: Gaussian isoperimetry and related topics II
The Gaussian isoperimetric inequality gives a sharp lower bound on the Gaussian surface area of any set in terms of its Gaussian measure. Its dimension-independent nature makes it a powerful tool for proving concentration inequalities in high dimensions. We will explore several consequence
From playlist Winter School on the Interplay between High-Dimensional Geometry and Probability

What is Stokes theorem? - Formula and examples
► My Vectors course: https://www.kristakingmath.com/vectors-course Where Green's theorem is a two-dimensional theorem that relates a line integral to the region it surrounds, Stokes theorem is a three-dimensional version relating a line integral to the surface it surrounds. For that reaso
From playlist Vectors

Assaf Rinot : Distributive Aronszajn trees
Abstract: It is well-known that the statement "all ℵ1-Aronszajn trees are special'' is consistent with ZFC (Baumgartner, Malitz, and Reinhardt), and even with ZFC+GCH (Jensen). In contrast, Ben-David and Shelah proved that, assuming GCH, for every singular cardinal λ: if there exists a λ+-
From playlist Logic and Foundations
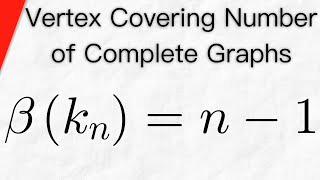
Vertex Covering Number of Complete Graphs | Graph Theory Exercises
We discuss and prove the vertex covering number of a complete graph Kn is n-1. That is, the minimum number of vertices needed to cover a complete graph is one less than its number of vertices. This is because, put simply, if we are missing at least 2 vertices in our attempted vertex cover,
From playlist Graph Theory Exercises

Lectures on compactness in the ̄∂–Neumann problem (Lecture 4) by Emil Straube
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Thm 1.10 - Probabilistic Version - part 06 - "Second Term"
Here we apply Jensen's inquality.
From playlist Theorem 1.10

Lectures on compactness in the ̄∂–Neumann problem (Lecture 5) by Emil Straube
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Hannah Larson - A refined Brill-Noether theory over Hurwitz spaces - AGONIZE miniconference
The celebrated Brill-Noether theorem says that the space of degree d maps of a general genus g curve to ℙr is irreducible. However, for special curves, this need not be the case. Indeed, for general k-gonal curves (degree k covers of ℙ1), this space of maps can have many components, of dif
From playlist Arithmetic Geometry is ONline In Zoom, Everyone (AGONIZE)

Thorben Kastenholz: Simplicial Volume of Total Spaces of Fiber Bundles
Thorben Kastenholz, University of Goettingen Title: Simplicial Volume of Total Spaces of Fiber Bundles It is a classical result that manifolds that are total spaces of fiber bundles, whose fiber has amenable fundamental group, have vanishing simplicial volume. In this talk I will explore t
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Matthew Kennedy: Noncommutative convexity
Talk by Matthew Kennedy in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on May 5, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)

"How to Verify the Riemann Hypothesis for the First 1,000 Zeta Zeros" by Ghaith Hiary
An overview of algorithms and methods that mathematicians in the 19th century and the first half of the 20th century used to verify the Riemann hypothesis. The resulting numerical computations, which used hand calculations and mechanical calculators, include those by Gram, Lindelöf, Backlu
From playlist Number Theory Research Unit at CAMS - AUB

Quenched large deviations for random motions in degenerate random media by Chiranjib Mukherjeer
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges
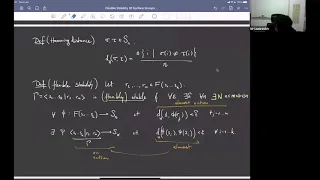
Surface groups are flexibly stable - Nir Lazarovich
Stability and Testability Topic: Surface groups are flexibly stable Speaker: Nir Lazarovich Affiliation: Technion Date: November 18, 2020 For more video please visit http://video.ias.edu
From playlist Stability and Testability
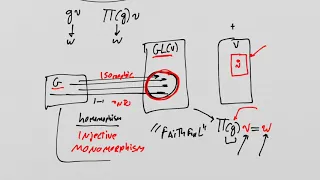
Lie Groups and Lie Algebras: Lesson 41: Elementary Representation Theory I
Lie Groups and Lie Algebras: Lesson 41: Elementary Representation Theory I I wanted to begin a more intricate example of the principle of a Universal Covering group, but I think I need to cover a little background material. We need to get a grip on what is meant by "Representation Theory"
From playlist Lie Groups and Lie Algebras