Infinitesimal model

Statistical models

The infinitesimal model, also known as the polygenic model, is a widely used statistical model in quantitative genetics. Originally developed in 1918 by Ronald Fisher, it is based on the idea that variation in a quantitative trait is influenced by an infinitely large number of genes, each of which makes an infinitely small (infinitesimal) contribution to the phenotype, as well as by environmental factors. In "The Correlation between Relatives on the Supposition of Mendelian Inheritance", the original 1918 paper introducing the model, Fisher showed that if a trait is polygenic, "then the random sampling of alleles at each gene produces a continuous, normally distributed phenotype in the population". However, the model does not necessarily imply that the trait must be normally distributed, only that its genetic component will be so around the average of that of the individual's parents. The model served to reconcile Mendelian genetics with the continuous distribution of quantitative traits documented by Francis Galton. The model allows genetic variance to be assumed to remain constant even when natural selection is occurring, because each locus makes an infinitesimal contribution to the variance. Consequently, all decline in genetic variance is assumed to be due to genetic drift. It also relies on the assumption of normal distributions, an assumption which breaks down if a trait is influenced by a finite number of loci. According to one research group, the model "...is obviously not an exact representation of the genome of any species, but is a useful assumption to make in genetic evaluation." Similarly, the model's assumption of infinitely many genes each with an infinitely small effect on the phenotype has been described as "practical but biologically unrealistic", and the genetic basis of evolutionary adaptation, contrary to the prediction of the model, often involves a modest number of loci of large effect. (Wikipedia).

Epsilon delta limit (Example 3): Infinite limit at a point

This is the continuation of the epsilon-delta series! You can find Examples 1 and 2 on blackpenredpen's channel. Here I use an epsilon-delta argument to calculate an infinite limit, and at the same time I'm showing you how to calculate a right-hand-side limit. Enjoy!

From playlist Calculus

How to develop a proper theory of infinitesimals I | Famous Math Problems 22a | N J Wildberger

Infinitesimals have been contentious ingredients in quadrature and calculus for thousands of years. Our definition of the term starts with the Wikipedia entry, modified a bit to reduce the dependence on "real numbers", which is actually quite unnecessary--- but as a logical definition it i

From playlist Famous Math Problems

Infinite Limits With Equal Exponents (Calculus)

#Calculus #Math #Engineering #tiktok #NicholasGKK #shorts

From playlist Calculus

Calculus 5.2c - Infinitesimals - Archimedes

Infinitesimals, what they are, and their early use by Archimedes. The Archimedes Palimpsest.

From playlist Calculus Chapter 5 (selected videos)

Fundamentals of Mathematics - Lecture 33: Dedekind's Definition of Infinite Sets are FInite Sets

https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html

From playlist Fundamentals of Mathematics

Difficulties with real numbers as infinite decimals ( I) | Real numbers + limits Math Foundations 91

There are three quite different approaches to the idea of a real number as an infinite decimal. In this lecture we look carefully at the first and most popular idea: that an infinite decimal can be defined in terms of an infinite sequence of digits appearing to the right of a decimal point

From playlist Math Foundations

Introduction to Infinite Limits in Calculus 1

From playlist Calculus 1 Exam 1 Playlist

Alison Etheridge & Nick Barton: Applying the infinitesimal model

The infinitesimal model is based on the assumption that, conditional on the pedigree, the joint distribution of trait values is multivariate normal, then, selecting parents does not alter the variance amongst offspring. We explain how the infinitesimal model extends to include dominance as

From playlist Probability and Statistics

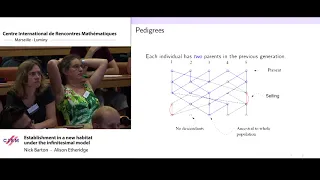
Nick Barton & Alison Etheridge: Establishment in a new habitat under the infinitesimal model

Abstract: Maladapted individuals can only colonise a new habitat if they can evolve a positive growth rate fast enough to avoid extinction - evolutionary rescue. We use the infinitesimal model to follow the evolution of the growth rate, and find that the probability that a single migrant c

From playlist Probability and Statistics

The True Power of Model Theory – Compactness, Infinitesimals and Ax's theorem

Thanks for watching! Go check out all submissions to 3blue1brown's contest: https://3b1b.co/SoME1 Corrections and remarks: none yet, let me know in the comments if you have any. Sources and resources: – First-order logic, compactness theorem David Marker's book: https://www.springer.com

From playlist Summer of Math Exposition Youtube Videos

Infinitely large numbers that act like they’re finite - Alok Singh

In this talk Alok gives a hands-on introduction to the idea of infinitely small and large numbers, in the framework of the hyperreals. He shows how this point of view allows you to do mathematics in a "natural" way with infinitely large numbers, including Taylor series expansions, differen

From playlist Anything At All seminar

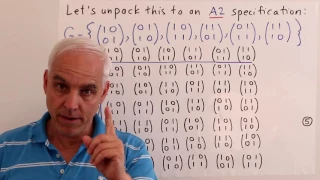
Logical challenges with abstract algebra II | Abstract Algebra Math Foundations 215 | NJ Wildberger

There is a very big jump in going from finite algebraic objects to "infinite algebraic objects". For example, there is a huge difference, if one is interested in very precise definitions, between the concept of a finite group and the concept of an "infinite group". We illustrate this imp

From playlist Math Foundations

Pablo Linares & Markus Tempelmayr - A tree-free construction of the structure group

We present a new approach to regularity structures, and in particular to the construction of the structure group, which replaces the tree-based framework of Hairer by a more Lie-geometric setting. We consider the space of pairs (a,p), where a is a placeholder for the nonlinearity and p is

From playlist Research Spotlight

Amandine Véber : The infinitesimal model of phenotypic evolution - a microscopic approach

The infinitesimal model of phenotypic evolution - a microscopic approach Recording during the meeting "IMathematical Models in Evolutionary Biology" the February 10, 2020 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this

From playlist Probability and Statistics

Conformal field theory and statistical mechanics (Lecture - 01)by John Cardy

Bangalore School on Statistical Physics - VIII DATE: 28 June 2017 to 14 July 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru This advanced level school is the eighth in the series. This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics in s

From playlist Bangalore School on Statistical Physics - VIII

A comparative analysis between two time-discretized versions of the... by Antonio Gómez Corral

DISCUSSION MEETING : MATHEMATICAL AND STATISTICAL EXPLORATIONS IN DISEASE MODELLING AND PUBLIC HEALTH ORGANIZERS : Nagasuma Chandra, Martin Lopez-Garcia, Carmen Molina-Paris and Saumyadipta Pyne DATE & TIME : 01 July 2019 to 11 July 2019 VENUE : Madhava Lecture Hall, ICTS, Bangalore

From playlist Mathematical and statistical explorations in disease modelling and public health

Benson Au: "Finite-rank perturbations of random band matrices via infinitesimal free probability"

Asymptotic Algebraic Combinatorics 2020 "Finite-rank perturbations of random band matrices via infinitesimal free probability" Benson Au - University of California, San Diego (UCSD) Abstract: Free probability provides a unifying framework for studying random multi-matrix models in the la

From playlist Asymptotic Algebraic Combinatorics 2020

The Infinite Monkey Theorem

Here's a re-enactment of the famous paradox known as the "infinite monkey theorem."

From playlist Cosmic Journeys

An algebraic infinitesimal approach to product and chain rules | FMP 22c | N J Wildberger

In this video we give the algebraic framework for a general infinitesimal approach to the Derivative of Faulhaber, valid for a general field F. We rely both on the notion of a dual complex number over F, and the idea of a bi-polynumber. Dual complex numbers are 2 x 2 matrices that incorpor

From playlist Famous Math Problems

Approximate cross validation for large data and high dimensions - Tamara Broderick, MIT

The error or variability of statistical and machine learning algorithms is often assessed by repeatedly re-fitting a model with different weighted versions of the observed data. The ubiquitous tools of cross-validation (CV) and the bootstrap are examples of this technique. These methods a

From playlist Statistics and computation

Infinitesimal model

Related pages