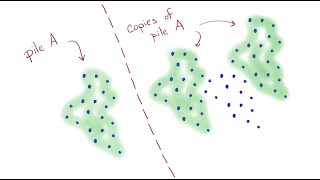
The Euclidean Algorithm: How and Why, Visually
We explain the Euclidean algorithm to compute the gcd, using visual intuition. You'll never forget it once you see the how and why. Then we write it out formally and do an example. This is part of a playlist on GCDs and the Euclidean algorithm: https://www.youtube.com/playlist?list=PLrm
From playlist GCDs and Euclidean algorithm

Jana Cslovjecsek: Efficient algorithms for multistage stochastic integer programming using proximity
We consider the problem of solving integer programs of the form min {c^T x : Ax = b; x geq 0}, where A is a multistage stochastic matrix. We give an algorithm that solves this problem in fixed-parameter time f(d; ||A||_infty) n log^O(2d) n, where f is a computable function, d is the treed
From playlist Workshop: Parametrized complexity and discrete optimization

Introduction to Number Theory (Part 4)
The Euclidean algorithm is established and Bezout's theorem is proved.
From playlist Introduction to Number Theory

Euclidean Algorithm and GCDs (Ex. 1)
This video gives an example of how and why the Euclidean algorithm is used to find the gcd of two numbers. Like so: gcd(x,y) = ?. -Here's a second example:http://youtu.be/CtUsUnHz9ek -Here's an example of using the Euclidean algorithm to find a multiplicative inverse: http://youtu.be/K5nb
From playlist Cryptography and Coding Theory

Tony Yue Yu - 4/4 The Frobenius Structure Conjecture for Log Calabi-Yau Varieties
Notes: https://nextcloud.ihes.fr/index.php/s/T6zEGCcJPS5JL4d 4/4 - Scattering diagram, comparison with Gross-Hacking-Keel-Kontsevich, applications to cluster algebras, applications to moduli spaces of Calabi-Yau pairs. --- We show that the naive counts of rational curves in an affine log
From playlist Tony Yue Yu - The Frobenius Structure Conjecture for Log Calabi-Yau Varieties

Euclidean Algorithm and GCDs (Ex. 2)
This video gives an example of how the Euclidean algorithm is used to find the gcd of two numbers. Like so: gcd(x,y) = ?. -Here's the first example: http://youtu.be/WA4nP-iPYKE -Here's a video for using the Euclidean algorithm to find a multiplicative inverse: http://youtu.be/K5nbGbN5Trs
From playlist Cryptography and Coding Theory
The extended Euclidean algorithm in one simple idea
An intuitive explanation of the extended Euclidean algorithm as a simple modification of the Euclidean algorithm. This video is part of playlist on GCDs and the Euclidean algorithm: https://www.youtube.com/playlist?list=PLrm9Y---qlNxXccpwYQfllCrHRJWwMky-
From playlist GCDs and Euclidean algorithm

GCD, Euclidean Algorithm and Bezout Coefficients
GCD, Euclidean Algorithm and Bezout Coefficients check out an earlier video on gcd. https://youtu.be/mQMksLNscY4
From playlist Elementary Number Theory

Membrane Excitability and Synaptic Plasticity (Lecture 1) by Suhita Nadkarni
PROGRAM ICTP-ICTS WINTER SCHOOL ON QUANTITATIVE SYSTEMS BIOLOGY (ONLINE) ORGANIZERS Vijaykumar Krishnamurthy (ICTS-TIFR, India), Venkatesh N. Murthy (Harvard University, USA), Sharad Ramanathan (Harvard University, USA), Sanjay Sane (NCBS-TIFR, India) and Vatsala Thirumalai (NCBS-TIFR, I
From playlist ICTP-ICTS Winter School on Quantitative Systems Biology (ONLINE)

Tony Yue Yu - 1/4 The Frobenius Structure Conjecture for Log Calabi-Yau Varieties
Notes: https://nextcloud.ihes.fr/index.php/s/GwJbsQ8xMW2ifb8 1/4 - Motivation and ideas from mirror symmetry, main results. --- We show that the naive counts of rational curves in an affine log Calabi-Yau variety U, containing an open algebraic torus, determine in a surprisingly simple wa
From playlist Tony Yue Yu - The Frobenius Structure Conjecture for Log Calabi-Yau Varieties

Béa de Laporte - Landau-Ginzburg potentials via projective representations
Many interesting spaces arise as partial compactifications of Fock-Goncharov's cluster varieties, among them (affine cones over) flag varieties which are important objects in representation theory of algebraic groups. Due to a construction of Gross-Hacking-Keel-Kontsevich those partial com
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

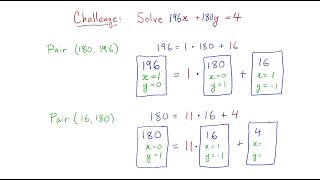
Extended Euclidean Algorithm to Solve Linear Diophantine Equation
#shorts #mathonshorts Check out the videos on the GCD, Euclidean algorithms here Two Basic Theorems on gcd (Greatest Common Divisors) of Two Integers (Bezout's Identity) https://youtu.be/mQMksLNscY4 An Example of GCD, and Extended Euclidean Algorithm In Finding the Bezout Coefficients h
From playlist Elementary Number Theory
If you are interested in learning more about this topic, please visit http://www.gcflearnfree.org/ to view the entire tutorial on our website. It includes instructional text, informational graphics, examples, and even interactives for you to practice and apply what you've learned.
From playlist Machine Learning

Winter School JTP: Homological mirror symmetry for log Calabi-Yau surfaces, Ailsa Keating
Given a log Calabi-Yau surface Y with maximal boundary D, I’ll explain how to construct a mirror Landau-Ginzburg model, and sketch a proof of homological mirror symmetry for these pairs when (Y,D) is distinguished within its deformation class (this is mirror to an exact manifold). I’ll exp
From playlist Winter School on “Connections between representation Winter School on “Connections between representation theory and geometry"

Some results on affine Deligne–Lusztig varieties – Xuhua He – ICM2018
Lie Theory and Generalizations Invited Lecture 7.8 Some results on affine Deligne–Lusztig varieties Xuhua He Abstract: The study of affine Deligne–Lusztig varieties originally arose from arithmetic geometry, but many problems on affine Deligne–Lusztig varieties are purely Lie-theoretic i
From playlist Lie Theory and Generalizations

An inverse theorem for the Gowers norms over finite fields - Ziegler
Tamar Ziegler Technion - Israel Institute of Technology June 18, 2010 For more videos, visit http://video.ias.edu
From playlist Mathematics

Michael Kemeny: The moduli of singular curves on K3 surfaces
In this talk we will study the moduli space Zg of smooth genus g curves admitting a singular model on a K3 surface. Using the Mori-Mukai approach of rank two, non-Abelian Brill-Noether loci we will work out the dimension of Zg, and further we will work out the Brill-Noether theory of curve
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Mod-05 Lec-37 Backward Induction
Game Theory and Economics by Dr. Debarshi Das, Department of Humanities and Social Sciences, IIT Guwahati. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist IIT Guwahati: Game Theory and Economics | CosmoLearning.org Economics
Chapter 4 - Solving Linear Equations with Technology - IB Math Studies (Math SL)
Hello and welcome to What The Math. This is a Chapter 4 video about linear equations and using GDC to solve various linear functions. This is a part of Chapter 4 from Harris Publication version of IB math book by Haese.
From playlist IB Math Studies Chapter 4

Tropical Lagrangian sections and Looijenga pairs - Andrew Hanlon
Joint IAS/Princeton University Symplectic Geometry Seminar Topic: Tropical Lagrangian sections and Looijenga pairs Speaker: Andrew Hanlon Affiliation: Stony Brook University Date: October 11, 2021 We will discuss the first steps in an approach to proving homological mirror symmetry for
From playlist Mathematics