
CCSS How to Label a Line, Line Segment and Ray
👉 Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure

Name the opposite rays in the given figure
👉 Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Overview of points lines plans and their location
👉 Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure

What is a point a line and a plane
👉 Learn essential definitions of points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A plane contains infinite number of lines. A ray is a li
From playlist Points Lines and Planes

Naming the rays in a given figure
👉 Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure

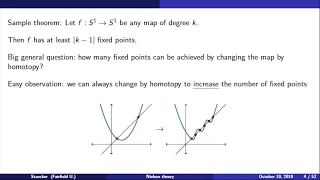
85 Years of Nielsen Theory: Fixed Points
Part 1 of a 3 part series of expository talks on Nielsen theory I gave at the conference on Nielsen Theory and Related Topics in Daejeon Korea, June 24, 2013. Part 2- Periodic Points: http://youtu.be/Ic26_F8UUBE Part 3- Coincidence Points: http://youtu.be/Wu2Cr3v_I44 Chris Staecker's int
From playlist Research & conference talks
Intro to Nielsen fixed point theory
A talk given by Chris Staecker at King Mongkut's University of Technology Thonburi, Bangkok, Thailand, on October 10 2019. Covers basic definitions and results of Nielsen fixed point theory, plus a few minutes about Nielsen-type theories for coincidence and periodic points. Should be und
From playlist Research & conference talks
Teena Gerhardt - 2/3 Algebraic K-theory and Trace Methods
Algebraic K-theory is an invariant of rings and ring spectra which illustrates a fascinating interplay between algebra and topology. Defined using topological tools, this invariant has important applications to algebraic geometry, number theory, and geometric topology. One fruitful approac
From playlist Summer School 2020: Motivic, Equivariant and Non-commutative Homotopy Theory

Symmetric spaces (Lecture – 02) by Pralay Chatterjee
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

Fixed points in digital topology
A talk given by Chris Staecker at King Mongkut's University of Technology Thonburi, Bangkok, Thailand, on October 11 2019. This is the second in a series of 3 talks given at KMUTT. Includes an introduction to graph-theoretical ("Rosenfeld style") digital topology, and some basic results a
From playlist Research & conference talks

Emanuele Dotto: Real topological Hochschild homology and the Hermitian K-theory...
Emanuele Dotto: Real topological Hochschild homology and the Hermitian K theory of Z2 equivariant rin The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. Real topological Hochschild homology (THR) is a Z/2-equivariant spectrum introd
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Name the segments in the given figure
👉 Learn how to label points, lines, and planes. A point defines a position in space. A line is a set of points. A line can be created by a minimum of two points. A plane is a flat surface made up of at least three points. A point is labeled using a capital letter. A line can be labeled usi
From playlist Labeling Point Lines and Planes From a Figure

Stefan Schwede: Equivariant stable homotopy - Lecture 2
I will use the orthogonal spectrum model to introduce the tensor triangulated category of genuine G-spectra, for compact Lie groups G. I will explain structural properties such as the smash product of G-spectra, and functors relating the categories for varying G (fixed points, geometric fi
From playlist Summer School: Spectral methods in algebra, geometry, and topology

Giuseppe De Nittis : Topological nature of the Fu-Kane-Mele invariants
Abstract: Condensed matter electronic systems endowed with odd time-reversal symmetry (TRS) (a.k.a. class AII topological insulators) show topologically protected phases which are described by an invariant known as Fu-Kane-Mele index. The construction of this in- variant, in its original f
From playlist Mathematical Physics

Victoria Hoskins: Group actions on quiver moduli spaces and applications
Abstract: We study two types of actions on King’s moduli spaces of quiver representations over a field k, and we decompose their fixed loci using group cohomology in order to give modular interpretations of the components. The first type of action arises by considering finite groups of qui
From playlist Algebraic and Complex Geometry

Yuan-Pin Lee - Introduction to Gromov-Witten theory (Part 2)
In these lectures, Gromov{Witten theory will be introduced, assuming only basic moduli theory covered in the rst week of the School. Then the Crepant Transformation Conjecture will be explained. Some examples, with emphasis on the projective/global cases, will be given. Note: The construct
From playlist École d’été 2011 - Modules de courbes et théorie de Gromov-Witten
