
Ring Theory: We define rings and give many examples. Items under consideration include commutativity and multiplicative inverses. Example include modular integers, square matrices, polynomial rings, quaternions, and adjoins of algebraic and transcendental numbers.
From playlist Abstract Algebra

Definition of a Ring and Examples of Rings
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Ring and Examples of Rings - Definition of a Ring. - Definition of a commutative ring and a ring with identity. - Examples of Rings include: Z, Q, R, C under regular addition and multiplication The Ring of all n x
From playlist Abstract Algebra

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

RNT1.2. Definition of Integral Domain
Ring Theory: We consider integral domains, which are commutative rings that contain no zero divisors. We show that this property is equivalent to a cancellation law for the ring. Finally we note some basic connections between integral domains and fields.
From playlist Abstract Algebra

Ring Examples (Abstract Algebra)
Rings are one of the key structures in Abstract Algebra. In this video we give lots of examples of rings: infinite rings, finite rings, commutative rings, noncommutative rings and more! Be sure to subscribe so you don't miss new lessons from Socratica: http://bit.ly/1ixuu9W ♦♦♦♦♦♦♦♦♦
From playlist Abstract Algebra
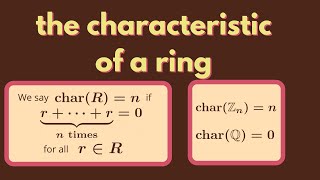
Abstract Algebra | The characteristic of a ring.
We define the characteristic of a ring and give some definitions. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

This lecture is part of an online course on rings and modules. We define Noetherian rings, give several equivalent properties, and give some examples of rings that are or are not Noetherian. This will be continued in the next lecture about Hilbert's finiteness theorems. For the other
From playlist Rings and modules

This lecture is part of an online course on rings and modules. We prove Hilbert's theorem that poynomial rings over fields are Noetherian, and use this to prove Hilbert's theorem about finite generation of algebras of invariants, at least for finite groups over the complex numbers. For
From playlist Rings and modules

Units in a Ring (Abstract Algebra)
The units in a ring are those elements which have an inverse under multiplication. They form a group, and this “group of units” is very important in algebraic number theory. Using units you can also define the idea of an “associate” which lets you generalize the fundamental theorem of ar
From playlist Abstract Algebra

Commutative algebra 4 (Invariant theory)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. This lecture is an informal historical summary of a few results of classical invariant theory, mainly to show just how complic
From playlist Commutative algebra

This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We define coherent modules over rings and coherent sheaves, and then discuss when the amps f* and f_* preserve coherence or quasicoherence.
From playlist Algebraic geometry II: Schemes

Commutative algebra 8 (Noetherian modules)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we define Noetherian modules over a ring, and use the to prove Noether's theorem that the agerba of invariants
From playlist Commutative algebra

Commutative algebra 24 Artinian modules
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We define Artinian rings and modules, and give several examples of them. We then study finite length modules, show that they
From playlist Commutative algebra

Schemes 16: Morphisms of finite type
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We introduce three properties of morphisms: quasicompact, finite type, and locally of finite type, and give a few examples.
From playlist Algebraic geometry II: Schemes

Commutative algebra 5 (Noetherian rings)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we find three equivalent ways of defining Noetherian rings, and give several examples of Noetherian and non-No
From playlist Commutative algebra

Commutative algebra 34 Geometry of normalizations
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We discuss the geometric meaning of finite morphisms and normal rings. Finite morphisms have the property that in the map of
From playlist Commutative algebra

Schemes 15: Quasicompact, Noetherian
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We define quasi-compact, Noetherian, and locally Noetherian schemes, give a few examples, and show that "locally Noetherian" is a local property.
From playlist Algebraic geometry II: Schemes

This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne.. We review valuation rings. We give a few examples of discrete and non-discrete valuation rings, and give a brief sketch of how non-discrete valuation rings us
From playlist Algebraic geometry II: Schemes