
What are Non-Classical logics?
Some of the general classes of non-classical logics I touch in this videos are linear logic, relevant logic, modal logic, many-valued logics, minimal logic, paraconsistent logics and so on and so forth. Let me know if I should dive deeping into a certain scene? https://en.wikipedia.org/wi
From playlist Programming

Fundamentals of Mathematics - Lecture 33: Dedekind's Definition of Infinite Sets are FInite Sets
https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html
From playlist Fundamentals of Mathematics
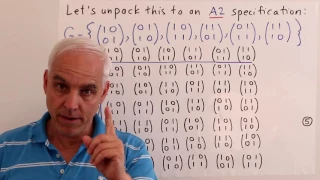
Logical challenges with abstract algebra II | Abstract Algebra Math Foundations 215 | NJ Wildberger
There is a very big jump in going from finite algebraic objects to "infinite algebraic objects". For example, there is a huge difference, if one is interested in very precise definitions, between the concept of a finite group and the concept of an "infinite group". We illustrate this imp
From playlist Math Foundations

Math 131 Fall 2018 092118 Cardinality
Recall definitions: injective, surjective, bijective, cardinality. Definitions: finite, countable, at most countable, uncountable, sequence. Remark: a 1-1 correspondence with the natural numbers is the same thing as a bijective sequence. Theorem: Every infinite subset of a countable set
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

Set Theory (Part 18): The Rational Numbers are Countably Infinite
Please feel free to leave comments/questions on the video and practice problems below! In this video, we will show that the rational numbers are equinumerous to the the natural numbers and integers. First, we will go over the standard argument listing out the rational numbers in a table a
From playlist Set Theory by Mathoma

From playlist Week 1 2015 Shorts

Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Mathematical Aspects of Computer Science

Logic: The Structure of Reason
As a tool for characterizing rational thought, logic cuts across many philosophical disciplines and lies at the core of mathematics and computer science. Drawing on Aristotle’s Organon, Russell’s Principia Mathematica, and other central works, this program tracks the evolution of logic, be
From playlist Logic & Philosophy of Mathematics

Thomas Colcombet : Algebra vs Logic over (generalised) words
CONFERENCE Recording during the thematic meeting : « Discrete mathematics and logic: between mathematics and the computer science » the January 17, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks give
From playlist Logic and Foundations

Introduction to the Cardinality of Sets and a Countability Proof
Introduction to Cardinality, Finite Sets, Infinite Sets, Countable Sets, and a Countability Proof - Definition of Cardinality. Two sets A, B have the same cardinality if there is a bijection between them. - Definition of finite and infinite sets. - Definition of a cardinal number. - Discu
From playlist Set Theory

We know that God exists because math is consistent and we know... - Kojman
Menachem Kojman Ben Gurion University of the Negev; Member, School of Mathemtics April 6, 2011 MATHEMATICAL CONVERSATIONS "We know that God exists because mathematics is consistent and we know that the devil exists because we cannot prove the consistency." -- Andre Weil For more videos,
From playlist Mathematics

Ivan Di Liberti - Towards higher topology
Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/DiLibertiSlidesToposesOnline.pdf We categorify the adjunction between locales and topological spaces, this amounts t
From playlist Toposes online

MIT 6.004 Computation Structures, Spring 2017 Instructor: Chris Terman View the complete course: https://ocw.mit.edu/6-004S17 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62WVs95MNq3dQBqY2vGOtQ2 6.2.1 Finite State Machines License: Creative Commons BY-NC-SA More inf
From playlist MIT 6.004 Computation Structures, Spring 2017

The True Power of Model Theory – Compactness, Infinitesimals and Ax's theorem
Thanks for watching! Go check out all submissions to 3blue1brown's contest: https://3b1b.co/SoME1 Corrections and remarks: none yet, let me know in the comments if you have any. Sources and resources: – First-order logic, compactness theorem David Marker's book: https://www.springer.com
From playlist Summer of Math Exposition Youtube Videos

Samson Abramsky - The sheaf-theoretic structure of contextuality and non-locality
Talk at the school and conference “Toposes online” (24-30 June 2021): https://aroundtoposes.com/toposesonline/ Slides: https://aroundtoposes.com/wp-content/uploads/2021/07/AbramskySlidesToposesOnline.pdf Quantum mechanics implies a fundamentally non-classical picture of the physical worl
From playlist Toposes online

Logic 8 - First Order Modus Ponens | Stanford CS221: Artificial Intelligence (Autumn 2021)
For more information about Stanford's Artificial Intelligence professional and graduate programs visit: https://stanford.io/ai Associate Professor Percy Liang Associate Professor of Computer Science and Statistics (courtesy) https://profiles.stanford.edu/percy-liang Assistant Professor
From playlist Stanford CS221: Artificial Intelligence: Principles and Techniques | Autumn 2021

Towards elementary infinity-toposes - Michael Shulman
Vladimir Voevodsky Memorial Conference Topic: Towards elementary infinity-toposes Speaker: Michael Shulman Affiliation: University of San Diego Date: September 13, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

Introduction to Predicate Logic
This video introduces predicate logic. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)

The big mathematics divide: between "exact" and "approximate" | Sociology and Pure Maths | NJW
Modern pure mathematics suffers from a major schism that largely goes unacknowledged: that many aspects of the subject are parading as "exact theories" when in fact they are really only "approximate theories". In this sense they can be viewed either as belonging more properly to applied ma
From playlist Sociology and Pure Mathematics