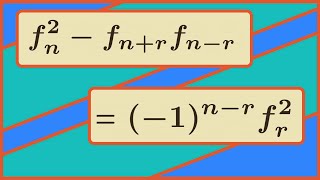
Catalan's Identity for Fibonacci Numbers
We prove Catalan's identity involving Fibonacci numbers using an interesting property of matrices known as the determinant sum property. This is similar to two other identities which we proved in the following videos: Cassini's Identity: https://youtu.be/pn0J0p0R_GM d'Ocagne's Identity: h
From playlist Identities involving Fibonacci numbers

Cassini's identity | Lecture 7 | Fibonacci Numbers and the Golden Ratio
Derivation of Cassini's identity, which is a relationship between separated Fibonacci numbers. The identity is derived using the Fibonacci Q-matrix and determinants. Join me on Coursera: https://www.coursera.org/learn/fibonacci Lecture notes at http://www.math.ust.hk/~machas/fibonacci.pd
From playlist Fibonacci Numbers and the Golden Ratio

An infinite product involving Fibonacci numbers!
After sketching two proofs of the closed form of the Fibonacci numbers, we find the value of an infinite product involving this famous sequence. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Identities involving Fibonacci numbers

Quadratic Identities (1 of 2: By comparison of coefficients)
More resources available at www.misterwootube.com
From playlist Polynomials (related content)

Fibonacci Mystery - Numberphile
Brady's view on people who write: "FIRST" - http://youtu.be/CmRh9tFYC68 More links & stuff in full description below ↓↓↓ Dr James Grime on the Pisano Period - a seemingly strange property of the Fibonacci Sequence. Available Brown papers: http://periodicvideos.blogspot.co.uk/2013/09/brow
From playlist James Grime on Numberphile

The Millin Series (A nice Fibonacci sum)
We derive the closed form for the Millin series, which involves reciprocals of the 2^nth Fibonacci numbers. We use Catalan's identity, the convergence of a subsequence, and the golden ratio. Catalan's Identity: https://youtu.be/kskAtiWC_w8 Another reciprocal Fibonacci sum: https://youtu.b
From playlist Identities involving Fibonacci numbers

STAIRS reveal the relationship between Fibonacci and combinatorics
Part I: https://youtu.be/Hl61mJxILA4 Source of the beautiful thumbnail: https://www.videoblocks.com/video/winter-stargate-deep-space-fibonacci-spiral-infinite-zoom-scl2tvcpliylych5s I am still surprised at why I have not thought of this more direct linkage between Fibonacci numbers and c
From playlist Fibonacci

Generating Functions and Combinatorial Identities
We describe one method of manipulating generating function to produce new combinatorial sum identities. We include an application of finding the value of a certain sum involving Fibonacci numbers. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Identities involving Fibonacci numbers

What do Fibonacci numbers have to do with combinatorics?
Part II: https://youtu.be/_RHXmGWXUvw Note: You ABSOLUTELY DON'T NEED TO HAVE KNOWN ANY COMBINATORICS because the combinatorics required in this video would be explained thoroughly. Source of the beautiful thumbnail: https://www.videoblocks.com/video/winter-stargate-deep-space-fibonacci-
From playlist Fibonacci

Decentralized Identity - Bonus Livestream Session
Decentralized Identity. it just sounds cool, right? But what is decentralized identity? Can you use it now? How might it be used in the future? Watch this video to learn about all of this and more! Chapters 0:00 Decentralized Identity Livestream Starts 1:04 Thank you Patrons 6:26 Introdu
From playlist Decentralization: DeFi, DID, DEX and more

Trig identities - What are they?
► My Trigonometry course: https://www.kristakingmath.com/trigonometry-course Trig identities are pretty tough for most people, because 1) there are so many of them, and 2) they’re hard to remember, and 3) it’s tough to recognize when you’re supposed to use them! But don’t worry, because
From playlist Trigonometry

How to Prove Trigonometric Identities (Precalculus - Trigonometry 24)
A very in-depth look at proving trigonometric identities. Several techniques are explored in many different examples of solving trig functions. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry

22C3: Digital Identity and the Ghost in the Machine
Speaker: Max Kilger "Once I Was Lost But Now I've Been Found" The demarcation line that used to separate your digital identity from your real world physical identity is rapidly disappearing. More seriously, it is permanently changing the way in which the world sees you and you see yourse
From playlist 22C3: Private Investigations

YOU CAN'T USE EULER'S IDENTITY TO PROVE THE ANGLE SUM IDENTITIES! | Tricky Parts of Calculus, Ep. 4
I give multiple proofs of the angle sum identities sin(x+y) = sin(x)cos(y) + sin(y)cos(x) and cos(x+y) = cos(x)cos(y) - sin(x)sin(y) from different perspectives. I stress that a very common presentation of these formulas based on Euler's identity e^(ix) = cos(x) + i sin(x) is circular and
From playlist Math

CERIAS Security: Protocols and Systems for Privacy Preserving Protection of Digital Identity 1/5
Clip 1/5 Speaker: Abhilasha Bhargav-Spantzel In this presentation I introduce a number of techniques that address the above problems. The approach is based on the concept of privacy preserving multi-factor identity verification. The main technique consists of verifying multiple identi
From playlist The CERIAS Security Seminars 2007

Introduction to Using Trigonometric Identities (Precalculus - Trigonometry 23)
A quick look at Trig Identities and how to use them. Basic identities such as the Pythagorean Identity, Reciprocal Identities, and Even/Odd Identities are explored. Support: https://www.patreon.com/ProfessorLeonard
From playlist Precalculus - College Algebra/Trigonometry


