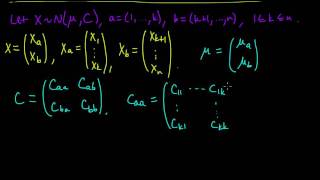Compound probability distributions | Continuous distributions
Exponentially modified Gaussian distribution
In probability theory, an exponentially modified Gaussian distribution (EMG, also known as exGaussian distribution) describes the sum of independent normal and exponential random variables. An exGaussian random variable Z may be expressed as Z = X + Y, where X and Y are independent, X is Gaussian with mean μ and variance σ2, and Y is exponential of rate λ. It has a characteristic positive skew from the exponential component. It may also be regarded as a weighted function of a shifted exponential with the weight being a function of the normal distribution. (Wikipedia).